В C++ любая функция кроме main() может вызывать саму себя. То есть в теле функции может быть размещен вызов этой же функции. Это называется рекурсией.
Когда программа выполняет код рекурсивной функции – она будет выполнять его бесконечно, если не предусмотреть условие выхода из рекурсии. Об этом надо помнить, чтобы избежать зацикливания вызовов. Поэтому в определении рекурсивной функции обязательно надо указывать условие выхода. Например, можно разместить её вызов внутри блока if.
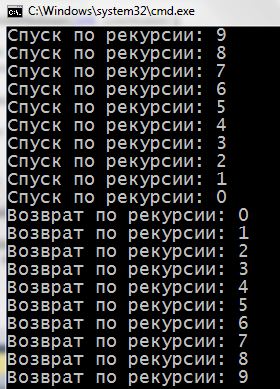
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(9); return 0; } |
В этой программе функция recursionGoDown() будет вызывать саму себя, пока в нее передается число больше нуля. Каждый раз, функция получает число, от которого в сигнатуре отнимается единица. Как только условие станет ложным (число станет меньше нуля) – вызовы остановятся и начнется выход из рекурсии.
Если мы передаем в такую функцию число 9, вызовов будет 10. Программа как бы углубляется на 10 уровней, выполняя рекурсию. Чтобы ей выйти из рекурсии, надо пройти эти десять уровней обратно. Так строка кода
1 | cout << "Возврат по рекурсии: " << someNumber << endl; |
будет выполняться тоже 10 раз, но значение someNumber будет меняться в обратном порядке. Сначала оно будет соответствовать тому, что передалось в функцию на 10 уровне рекурсии, потом тому что передалось на 9 уровне и т.д.
Хочу обратить внимание на важный момент. При каждом рекурсивном вызове создается новая переменная someNumber с новым значением. Эти переменные будут занимать какое-то место в оперативной памяти. Если вызовов 10, как в нашем примере, то и в памяти будет храниться 10 переменных с разными значениями. Можно дописать в программу вывод на экран адресов, по которым хранятся эти значения и убедиться в этом:
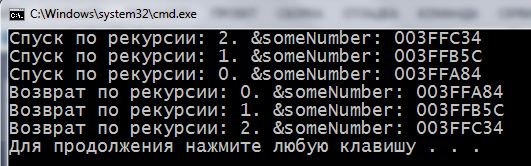
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(2); return 0; } |
Передаем в функцию число 2: recursionGoDown(2); Уровней рекурсии будет 3.
Как видно, каждое значение переменной someNumber хранится в отдельном отрезке памяти. Во время обратного выхода по рекурсии значения берутся из тех же адресов но в обратном порядке.
Практически каждую поставленную задачу, которую можно решить используя рекурсию, можно реализовать используя итерации циклов. Вы ведь легко можете показать на экран числа от 9 до 0 и от 0 до 9 применив циклы. Помимо этого следует знать, что рекурсия займет больше памяти и будет производить вычисления медленнее, чем итерация.
Но, как утверждают опытные программисты и многие авторы книг, это не значит, что рекурсия бесполезна. Есть задачи, решать которые, используя итерации циклов, сложно и громоздко. А рекурсивное решение выглядит лучше. Для начального уровня, пока вы изучаете только основы программирования на C++, вам достаточно просто понимать, что из себя представляет рекурсия и как она работает.
Посмотрите ещё видео по теме Рекурсия:
Вы слишком строги к рекурсии ;-)
1. Рекурсия – это общий математический аппарат, которым теоретически выражаются все вычислимые алгоритмы (это я взял из мат. теории алгоритмов).
2. Все задачи над динамическими структурами данных (списки, очереди, деревья, графы, …) решаются рекурсивно проще, а главное нагляднее, чем итерационно (итерационные циклические алгоритмы лучше работают над массивами – статическими конструкциями).
3. Есть алгоритмы, которые выражаются в 2-3 строчки рекурсивно, но которые крайне сложно выписать без рекурсии. Красивейший пример тому: знаменитая задача “Ханойская башня”. Многие алгоритмы сортировки (тех же массивов) лучше выражаются в рекурсивной форме.
Рекурсия только кажется сложной, потому что ей не учат в отечественной практике и не умеют её применять. А в университетах Франции, например, обучение 1-го семестра начинают с обучения рекурсивным алгоритмам.
Всегда хорошо, когда кто-то высказывает свою точку зрения и свое личное мнение, основанное на опыте. Начинающим полезно будет почитать.
Как вы предлагаете использовать рекурсию в списках и очередях?
Рекурсия – это самый естественный способ обработки любых динамических структур (списков, деревьев и т.д.), это демонстрируют функциональные языки программирования, такие как Lisp. Такой подход намного эффективней, чем итерационный (циклами). Но это нужно показывать на примерах кода…
А простой и красивый пример рекурсии посмотрите в задаче возведения числа в степень: https://purecodecpp.com/archives/2734
Здравствуйте.
Объясните пожалуйста следующие моменты, всю голову сломал, не могу понять:
1. Если в массив в процессе деления на подмассивы не длиться ровно на 2, то программа прекратит работу? Ведь в int middle= arr[(l+r)]/2 , где (l+r)/2- целое число.
2. Если в массиве есть повторяющиеся числа, и у опорного элемента будет такое же число, как у числа слева или справа, например 1,2,3, 5, 6,5,7
то, не получится что после того, как программа определила центральный элемент =5, и начала его сравнение с элементами правого подмассива , она дойдя до одинакового элемента arr [5]=5 подумает что достигла центрального элемента , перестанет сравнивать более ранние элементы (arr [4}, arr [3]) с центральным, примет этот 5 элемент за центральный, и далее будет считать его крайней левой границей?
3. В примере рассматривалась попарная смена (слева и справа от центрального) элементов, не удовлеторяющих условию:
while (middle>arr [i]) i++;
while (middle<arr [j]) j–;
if (i<=j)
{
swap (arr [i], arr [j]);
i++;
j–;
}
А что если либо изначально, либо после процесса сортировки остался 1
подлежащий замене элемент, например:
1, 2, 3, 8, 5, 6, 7, 9,10
то если я правильно понял, он поменяется с центральным элементом,
т.е. получится 1,2,3,5, 8, 6,7,9,10 ?
4.
Значение центрального элемента может поменяется. В то же время после такого изменения центрального элемента, сравнения, произведенные с более ранним центральным элементом окажутся неверными, т.к они не пересматриваются, и продолжают идти дальше. В результате сортировка окажется неверной.
Например:
исходный массив: 1,2,6,9, 4, 10,11,3, 12 с центральным элементом 4.
После первой замены (6 на 3) получается: 1,2,3,9, 4, 10,11,6,12.
После второй замены (9 на 4) получается: 1,2,3,4, 9, 10,11,6,12 и сортировка этого множества заканчиватся. Однако элемент правого подмножества 6 отсортирован неправильно.
интересно, я освоил рекурсию и вот начал уже решать задачки на эту тему с сайта acmp.ru, и вот на такую задачу наткнулся:
Сумма кубов
(Время: 1 сек. Память: 16 Мб Сложность: 52%)
Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел. Вася решил придумать аналогичное утверждение для кубов – он хочет узнать, сколько кубов достаточно для представления любого числа. Его первая рабочая гипотеза – восемь.
Выяснилось, что почти все числа, которые Вася смог придумать, представляются в виде суммы не более чем восьми кубов. Однако число 239, например, не допускает такого представления. Теперь Вася хочет найти какие-либо другие такие числа, а также, возможно, какую-либо закономерность в представлениях всех остальных чисел, чтобы выдвинуть гипотезу относительно вида всех чисел, которые не представляются в виде суммы восьми кубов.
Помогите Васе написать программу, которая проверяла бы, возможно ли представить данное натуральное число в виде суммы не более чем восьми кубов натуральных чисел, и если это возможно, то находила бы какое-либо такое представление.
Входные данные
Во входном файле INPUT.TXT записано натуральное число N (1 ≤ N ≤ 2×109).
Выходные данные
В выходной файл OUTPUT.TXT выведите не более восьми натуральных чисел в порядке невозрастания, кубы которых в сумме дают N. Если вариантов несколько, то выведите любой. Если искомого представления не существует, то в выходной файл необходимо вывести слово IMPOSSIBLE.
Примеры
№ INPUT.TXT OUTPUT.TXT
1 17 2 2 1
2 239 IMPOSSIBLE
Думал что дп и даже код написал, а позже понял что вектора такого размера просто не существует, пожалуйста помогите решить данную задачу
Непонятно, почему рекурсия начинает выдавать значения в обратном порядке, в коде ничего такого не видно:
void recursionGoDown(int someNumber)
{
cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber < 0)
{
recursionGoDown(someNumber – 1); // рекурсивный вызов
}
cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl;
}
По-идее, как только someNumber делается равным 0, условие оператора if становится ложным и блок {recursionGoDown(someNumber – 1);} должен просто игнорироваться. Но вместо этого он выполняется в обратном порядке. Как это дерьмо устроено???
qht9a9