Алгоритм сортировки массива “пузырьковая сортировка” рассматривается практически во всех учебниках по программированию на С++. Его легко понять начинающим. Он наглядный и очень простой.
На практике этот алгоритм почти никто не использует, так как он медлительный и есть более быстрые и усовершенствованные алгоритмы. Мы также разберем его потому, что сортировка “пузырьком” – это основа некоторых более эффективных алгоритмов, которые будут изложены в следующих статьях. Это “быстрая” сортировка, “пирамидальная” сортировка и “шейкерная” сортировка.
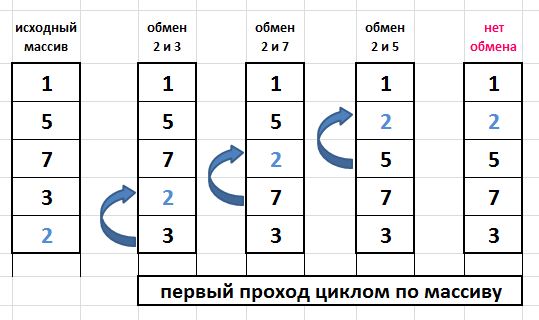
Как работает “пузырьковая” сортировка? Допустим у нас есть неотсортированный массив чисел из 5-ти элементов и нам предстоит разместить значения по возрастанию. Для наглядности, на рисунке изобразим этот массив вертикально “Исходный массив”.
Алгоритм сортировки “пузырьком” состоит в повторении проходов по массиву с помощью вложенных циклов. При каждом проходе по массиву сравниваются между собой пары “соседних” элементов. Если числа какой-то из сравниваемых пар расположены в неправильном порядке – происходит обмен (перезапись) значений ячеек массива.
Образно говоря в нашем примере 2 “легче” чем 3 – поэтому обмен есть, далее 2 “легче” чем 7 – снова обмен и т.д. При сравнении нулевого и первого элемента на нашем рисунке обмена нет, так как 2 “тяжелее” чем 1. Таким образом более “легкое” значение, как пузырек в воде, поднимается вверх до нужной позиции. Вот почему у этого алгоритма такое название.
Рассмотрим алгоритм сортировки “пузырьком” в работе:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | #include <iostream> using namespace std; // прототип функции, которая выполнит сортировку "пузырьком" void bubbleSort(int arrForSort[], const int SIZE); void main() { setlocale(LC_ALL, "rus"); const int SIZE = 5; int arr[SIZE]; cout << "Исходный массив:\n"; for (int i = 0; i < SIZE; i++) { arr[i] = SIZE - i; // заполняем значениями по убыванию cout << arr[i] << "\n__\n"; } cout << "\n\n"; bubbleSort(arr, SIZE); // передаем в функцию для сортировки cout << "Массив после сортировки:\n"; for (int i = 0; i < SIZE; i++) { cout << arr[i] << "\n__\n"; } cout << "\n\n"; } void bubbleSort(int arrForSort[], const int SIZE) { int buff = 0; // для временного хранения значения, при перезаписи for (int i = 0; i < SIZE - 1; i++) // { // вложенный цикл проходит от четвертого элемента // до первого, находит с помощью if самое "легкое" значение, // сравнивая соседние пары элементов, // и поднимает его в нулевую ячейку массива for (int j = SIZE - 1; j > i; j--) { if (arrForSort[j] < arrForSort[j - 1]) { buff = arrForSort[j - 1]; arrForSort[j - 1] = arrForSort[j]; arrForSort[j] = buff; } } // далее значение i увеличивается на 1 // и внутренний цикл будет перебирать элементы // от четвертого до второго. Таким образом поднимет самое // "легкое" значение из оставшихся в первую ячейку и т.д. } } |
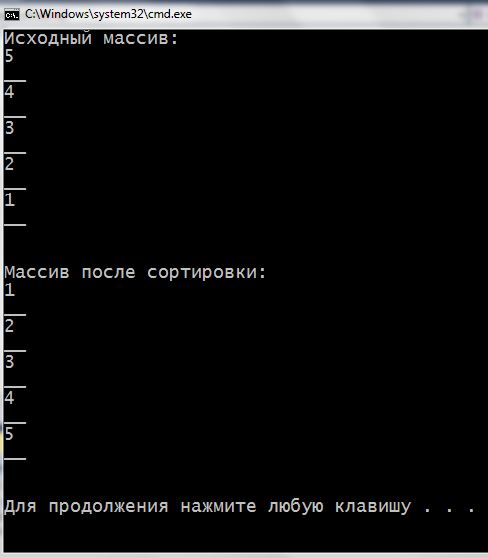
Внимательно разобрав данный пример с подробными комментариями, вам должно быть все понятно. Результат на экране такой:
Дополнить можно следующим: после того, как внутренний цикл отработает один раз, минимальное значение массива будет занимать нулевую ячейку. Поэтому при повторном проходе, очередное минимальное значение из оставшихся надо будет разместить в следующей ячейке (i + 1).
Таким образом нет необходимости сравнивать между собой все элементы массива снова и количество обрабатываемых значений уменьшается на 1. При сортировке “пузырьком” необходимо пройти SIZE – 1 итераций внешнего цикла, так как сравнивать один элемент с самим собой – смысла нет.
Не будем забывать то, о чем мы говорили в самом начале – алгоритм “пузырьковой” сортировки малоэффективен и медлителен. Если у нас есть частично отсортированный массив и необходимо переместить в начало только одно значение, он все равно будет проходить все итерации циклов. То есть производить сравнение уже отсортированных значений массива, хотя этого уже можно и не делать.
Давайте немного улучшим эту ситуацию. Добавим в код еще одну переменную-“флажок”, которая будет давать знать, произошел ли обмен значений на данной внешнего цикла итерации или нет. Перед тем, как войти во внутренний цикл, “флажок” будет сбрасываться в 0.
Если обмен значениями в этом цикле случится – “флажку” будет присвоено значение 1, если нет – то он останется равным 0. В последнем случае (если “флажок” равен 0) – обменов не было и массив полностью отсортирован. Поэтому программе можно досрочно выйти из циклов, чтобы не тратить время попусту на последующие ненужные сравнения.
Рассмотрите следующий пример:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 | #include <iostream> using namespace std; void bubbleSort(int arrForSort[], const int SIZE); int main() { setlocale(LC_ALL, "rus"); const int SIZE = 5; int arr[SIZE] = {3, 4, 2, 5, 6}; cout << "Исходный массив:\n"; for (int i = 0; i < SIZE; i++) { cout << arr[i] << "\n__\n"; } cout << "\n\n"; bubbleSort(arr, SIZE); cout << "Массив после сортировки:\n"; for (int i = 0; i < SIZE; i++) { cout << arr[i] << "\n__\n"; } cout << "\n\n"; return 0; } void bubbleSort(int arrForSort[], const int SIZE) { int buff = 0; int f; // "флаг" for (int i = 0; i < SIZE - 1; i++) { f = 0; for (int j = SIZE - 1; j > i; j--) { if (arrForSort[j] < arrForSort[j - 1]) { buff = arrForSort[j - 1]; arrForSort[j - 1] = arrForSort[j]; arrForSort[j] = buff; /* если хоть одна пара значений былы расположена неправильно то есть условие if - верно, то присваиваем флагу значение 1*/ f = 1; } } // если массив отсортирован и замен не было // то есть f осталось равным 0 - прерываем цикл if (f == 0) break; // для себя показываем количество проходов по массиву вложенным циклом cout << i + 1 << "!!! \n"; } cout << endl; } |
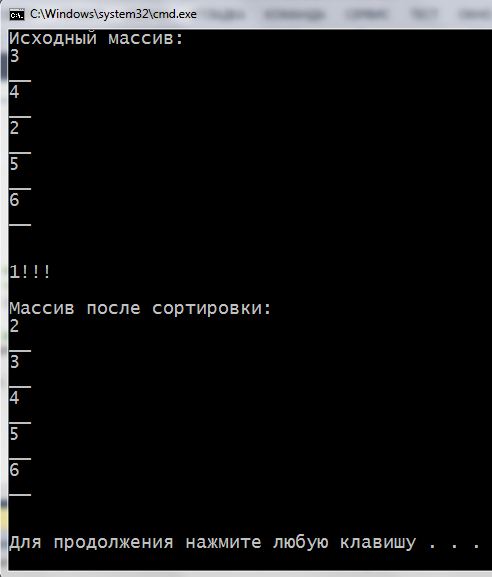
Видим такую картину после запуска:
Видно что программа прошла вложенным циклом по массиву 1 раз, переместила значение 2 в нужное место и завершила работу. А вот, что будет на экране, если закомментировать все строки кода, где есть переменная-“флажок”:
Программа вхолостую 4 раза “гоняла” по массиву, хотя значение 2 перемещено в нужную ячейку еще при первом проходе вложенным циклом.
В сети есть прикольное видео (автор: AlgoRythmics ). В нем представлена “пузырьковая” сортировка в усовершенствованном варианте (когда отсортированные элементы массива уже не сравниваются между собой). Единственное – в наших примерах сравнение значений начиналось с последнего элемента. А в предложенном видео – от нулевого к последнему. Посмотрите и увидите, как элементы перемещаются в массиве на нужные места :)

Добрый день.
Помогите, пожалуйста разобраться в методе, ломаю голову не могу понять принцип двух вложенных циклов.
Есть код:
#include
#include
using namespace std;
int main()
{
setlocale(LC_ALL, “Russian”);
int nums[10];
int a,b,t;
int size;
size = 10; // Количество сортируемых элементов.
// Помещаем массив случайные числа.
for(t=0; t<size; t++) nums[t] = rand();
// Отображаем исходный массив.
cout << "Исходный массив:\n ";
for(t=0; t<size; t++) cout << nums[t] << ' ';
cout << '\n';
//Реализация алгоритма пузырьковой сортировки.
for(a=1; a=a; b–) {
if(nums[b-1] > nums[b]) { // Если значения элементов массива
// расположены не по порядку,
// то меняем их местами.
t = nums[b-1];
nums[b-1] = nums[b];
nums[b] = t;
}
}
// Отображаем отсортированный массив.
cout << "\n Отсортированный массив:\n ";
for(t=0; t<size; t++) cout << nums[t] << ' ';
system("pause");
return 0;
}
Интересует:
for(a=1; a=a; b–) {
if(nums[b-1] > nums[b]) { // Если значения элементов массива
// расположены не по порядку,
// то меняем их местами.
t = nums[b-1];
nums[b-1] = nums[b];
nums[b] = t;
}
}
Почему в цикле for(a=1; a<size; a++) a<siz а не a=a; b–) не могу разобрать.
И последнее
t = nums[b-1];
nums[b-1] = nums[b];
nums[b] = t;
Можно ли как-нибудь упростить замену?
Добрый день.
Помогите, пожалуйста, разобраться в методе. Голову ломаю, не могу понять.
Есть код с книжки:
#include
#include
using namespace std;
int main()
{
setlocale(LC_ALL, “Russian”);
int nums[10];
int a,b,t;
int size;
size = 10; // Количество сортируемых элементов.
// Помещаем массив случайные числа.
for(t=0; t<size; t++) nums[t] = rand()%100;
// Отображаем исходный массив.
cout << "Исходный массив:\n ";
for(t=0; t<size; t++) cout << nums[t] << ' ';
cout << '\n';
//Реализация алгоритма пузырьковой сортировки.
for(a=1; a=a; b–) {
if(nums[b-1] > nums[b]) { // Если значения элементов массива
// расположены не по порядку,
// то меняем их местами.
t = nums[b-1];
nums[b-1] = nums[b];
nums[b] = t;
}
}
// Отображаем отсортированный массив.
cout << "\n Отсортированный массив:\n ";
for(t=0; t<size; t++) cout << nums[t] << ' ';
system("pause");
return 0;
}
Больше всего волнует вложенные циклы:
for(a=1; a=a; b–)
Во внешнем цикле почему a<size а не a=a что это такое и как оно работает?
И последнее:
Подскажите, как можно упросить перестановку:
t = nums[b-1];
nums[b-1] = nums[b];
nums[b] = t;
> Подскажите, как можно упростить перестановку:
А что там упрощать?
В C, C++ и подобным им языках (Pascal, Java и др.) обменять значения 2-х переменных (a и b) можно только чере 3-ю промежуточную переменную (c):
c = a;
a = b;
b = c; // а и b поменялись значениями
В более высокоуровневых языках, таких как Python или Go, это можно было бы записать проще:
a, b = b, a
Можно упростить с помощю ф-цыи swap() ;
swap(arrForSort[j],arrForSort[j-1]);
Можно записать через функцию swap() … только это вряд ли можно считать упрощением, потому что в этой функции делается то же самое.
но как минимум не нужно вводить 3 переменную
А в чём разница ? … от одной лишней переменной…
Когда речь перейдёт от совершенно элементарных задач к более-менее обстоятельным, то один-два десятка переменных больше или меньше – перестают играть какую-то роль. Там вступают в игру другие критерии.
Про алгоритм пузырьковой сортировки нужно бы ещё запомнить то, что это наихудший (в смысле эффективности, числа операций) алгоритм сортировки из всех известных.
Но соискатели на собеседованиях и студенты на экзаменах упортно “тулят” именно этот метод.
В этом есть какая-то загадка…
Да это привычка обычная. Метод самый простой для понимания, вот и тулят его везде.