Рассмотрев “пузырьковую” сортировку массива можно перейти к разбору её разновидности – “шейкер”-сортировке. Вы можете встретить несколько её названий : сортировка перемешиванием, пульсирующая сортировка, двунаправленная сортировка “пузырьком”.
Внимательно присмотревшись к тому, как проходит сортировка “пузырьком” – можно сказать следующее: часть массива, в котором перестановки элементов уже не происходят (отсортированная часть массива), то эту часть можно исключить из рассмотрения и не обрабатывать на следующих итерациях. Второе, что вы могли заметить – это то, что минимальный (самый “легкий” элемент) при сортировке сразу перемещается в самое начало массива, а “тяжелые” элементы сдвигаются только на одну позицию “вниз”. Так массив
будет отсортирован за один проход вложенным циклом, а для массива
понадобится три итерации.
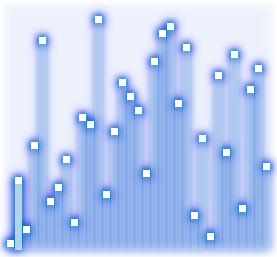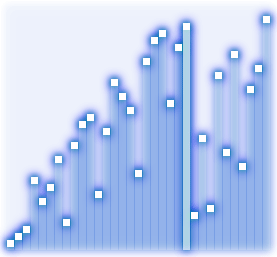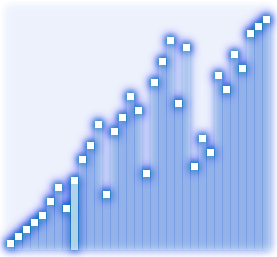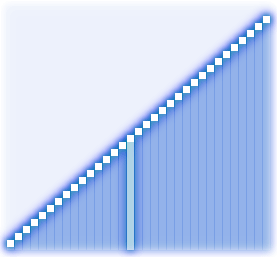
Поэтому была придумана более эффективная форма сортировки “пузырьком” -“шейкер”-сортировка. В ней пределы той части массива в которой есть перестановки, сужаются. Плюс – внутренние циклы проходят по массиву то в одну, то в другую сторону, поднимая самый легкий элемент вверх и опуская самый тяжелый элемент в самый низ за одну итерацию внешнего цикла. Набирайте код:
Рассмотрим саму функцию в которой происходит “шейкер”-сортировка (двунаправленная сортировка “пузырьком”) – строки 14-31. Благодаря переменным leftMark и rightMark участок массива, который подлежит сортировке будет сужаться с каждым шагом цикла. Это положительно скажется на времени работы программы. А благодаря двум вложенным циклам for – за одну итерацию внешнего цикла минимальное и максимальное значения займут свои правильные позиции в массиве.
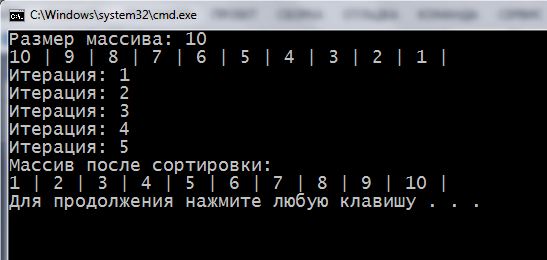
Результат:
Как и говорилось, на выполнение сортировки массива по возрастанию понадобилось в два раза меньше итераций внешнего цикла по сравнению с классической “пузырьковой” сортировкой.
Почитайте также о других алгоритмах сортировок данных.
Зачем в условии while (leftMark <= rightMark) (строка 18) проверка на равенство? Ведь в случае равенства левой и правой границ остался 1 элемент, и для него прохождение лишней итерации не требуется.
Чем шейкерная сортировка эффективнее? – тем что за одну итерацию внешнего цикла не только наименьший элемент перемещается вниз, но и наибольший – вверх? – дак зато сама итерация стала сложнее.
Т.е. в худшем случае пузырьковой сортировки было N итераций внешнего цикла, каждая из которых выполняла N-i итераций внутреннего (где i – номер итерации внешнего цикла). Т.е. сложность вычисляется как сумма (N-i) для всех i от 1 до N, т.е. N * (N+1)/2 = 0.5*N^2 + 0.5*N. Асимптотически – это N^2, но формулу пишу такую, т.к. более точная (может быть так у шейкера хоть какое-то преимущество появится?)
В худшем случае шейкерной сортировки будет выполнено N/2 итераций внешнего цикла (ведь за одну итерацию 2 элемент занимают свои места в отсортированном массиве), а вот внутренний цикл имеет сложность (N-i) * 2. Сложность сортировки – это сумма (N-i)*2 для всех i от 1 до N/2. Опять видим арифметическую прогрессию и считаем сумму как
N * ((N-1) + (N-N/2))/2 = N * (N-1 + N – N/2)/2 = (1.5*N*N-N)/2 = 0.75*N^2 – N/2.
Дак вот даже если отбросить анализ при N стремящемся к бесконечности (где сортировки эквиваленты по эффективности), очевидно же, что для небольших значений N “оптимизированный” алгоритм будет работать хуже (по крайней мере в худшем случае).
Где я сейчас неправильно посчитал? – никогда не понимал всех этих свистоплясок с шейкером.
Шейкерная сортирует почти отсортированный массив за O(n)
В коде утечка памяти
shtrafnie = [6, 10, 3, 5, 8]
link_shtraf = {
6: [‘Карелин’, ‘Александр’, ‘Российская сборная’, ‘Борьба классического стиля’, ’10’],
10: [‘Попов’, ‘Александр’, ‘Олимпийская сборная’, ‘Плавание’, ’15’],
3: [‘Ищенко’, ‘Наталья’, ‘Олимпийская сборная’, ‘Синхронное плавание’, ’13’],
5: [‘Шарапова’, ‘Мария’, ‘-Нет-‘, ‘Теннис’, ’10’],
8: [‘Аршавин’, ‘Андрей’, ‘Арсенал’, ‘Футбол’, ’10’]
}
def insertion(data):
for i in range(len(data)):
j = i – 1
key = data[i]
while data[j] > key and j >= 0:
data[j + 1] = data[j]
j -= 1
data[j + 1] = key
return data
def shaker_sort(array):
length = len(array)
swapped = True
start_index = 0
end_index = length – 1
while (swapped == True):
swapped = False
# проход слева направо
for i in range(start_index, end_index):
if (array[i] > array[i + 1]) :
# обмен элементов
array[i], array[i + 1] = array[i + 1], array[i]
swapped = True
# если не было обменов прерываем цикл
if (not(swapped)):
break
swapped = False
end_index = end_index – 1
#проход справа налево
for i in range(end_index – 1, start_index – 1, -1):
if (array[i] > array[i + 1]):
# обмен элементов
array[i], array[i + 1] = array[i + 1], array[i]
swapped = True
start_index = start_index + 1
return array
for i in shtrafnie:
print(f’Фамилия: {link_shtraf[i][0]}, Имя: {link_shtraf[i][1]}, Команда: {link_shtraf[i][2]}, Вид спорта: {link_shtraf[i][3]}, Зачётный результат: {link_shtraf[i][4]}’)
insertion(shtrafnie)
print(‘—–Сортировка простыми вставками—–‘)
for i in shtrafnie:
print(f’Фамилия: {link_shtraf[i][0]}, Имя: {link_shtraf[i][1]}, Команда: {link_shtraf[i][2]}, Вид спорта: {link_shtraf[i][3]}, Зачётный результат: {link_shtraf[i][4]}’)
print(‘—–Сортирую Шейкер сортировкой—–‘)
shaker_sort(shtrafnie)
for i in shtrafnie:
print(f’Фамилия: {link_shtraf[i][0]}, Имя: {link_shtraf[i][1]}, Команда: {link_shtraf[i][2]}, Вид спорта: {link_shtraf[i][3]}, Зачётный результат: {link_shtraf[i][4]}’)