Сортировка вставками С++ (видео)

Еще одним алгоритмом, разработанным для упорядочивания массивов, является алгоритм Сортировка вставками (Insertion Sort). Этот алгоритм (как и другие, рассматриваемые на нашем сайте) достаточно прост. Он состоит из двух циклов (один вложен в другой). Первый цикл производит проход по массиву, а второй – перемещение обрабатываемых элементов. Давайте сразу посмотрим, как может выглядеть код такой сортировки, а уже ниже разберем, как он работает.

#include <iostream>
using namespace std;

int main()
{
	const int N = 10;
	int a[N] = { 12, 5, 3, 2, 45, 96, 6, 8, 11, 24 };

	int buff = 0;	// для хранения перемещаемого значения
	int i, j;		// для циклов		

	/************* Начало сортировки *******************/
	for (i = 1; i < N; i++)
	{
		buff = a[i]; // запомним обрабатываемый элемент
		// и начнем перемещение элементов слева от него
		// пока запомненный не окажется меньше чем перемещаемый
		for (j = i - 1; j >= 0 && a[j] > buff; j--)
					a[j + 1] = a[j];	

		a[j + 1] = buff; // и поставим запомненный на его новое место	
	}
	/************* Конец сортировки *******************/

	for (int i = 0; i < N; i++) // вывод отсортированного массива
		cout << a[i] << '\t';
	cout << endl;
}

#include <iostream>

using namespace std;

int main()

{

const int N = 10;

int a[N] = { 12, 5, 3, 2, 45, 96, 6, 8, 11, 24 };

int buff = 0; // для хранения перемещаемого значения

int i, j; // для циклов

/************* Начало сортировки *******************/

for (i = 1; i < N; i++)

{

buff = a[i]; // запомним обрабатываемый элемент

// и начнем перемещение элементов слева от него

// пока запомненный не окажется меньше чем перемещаемый

for (j = i - 1; j >= 0 && a[j] > buff; j--)

a[j + 1] = a[j];

a[j + 1] = buff; // и поставим запомненный на его новое место

}

/************* Конец сортировки *******************/

for (int i = 0; i < N; i++) // вывод отсортированного массива

cout << a[i] << '\t';

cout << endl;

}

Алгоритм Сортировка вставками можно описать следующими позициями:

Запомнить во временную переменную ( buff в примере) значение текущего элемента массива;
Пока элементы слева от запомненного значения больше чем запомненное – перемещаем их на позицию вправо. Получается, что предыдущий элемент займет ячейку запомненного. А тот, что стоит перед предыдущим – переместится в свою очередь на место предыдущего. И так элементы будут двигаться друг за дружкой.
Движение элементов заканчивается, если очередной элемент, который нужно сдвинуть, оказывается по значению меньше, чем тот, что запомнили во временную переменную в начале цикла.
Цикл берет следующий элемент, и опять сдвигает все, которые расположены перед ним и большие по значению.

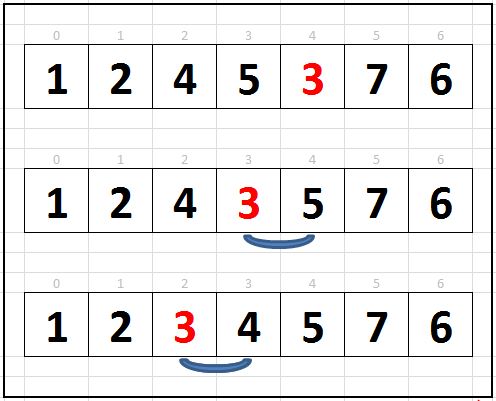
Покажем визуально перемещение значения в массиве из семи элементов во время работы Сортировки вставками:

На первой итерации в переменную-буфер запишется значение из ячейки с индексом 1 и цикл будет проверять этот элемент. Там у нас находится число 2. Оно больше значения, которое записано в нулевой ячейке, поэтому перемещений не будет. Далее в переменную-буфер запишется значение из ячейки с индексом 2 и снова пойдет сравнение со значениями слева и т.д. Только на четвертой итерации внешнего цикла начнется перезапись значений. Тройка сначала поменяется местами с пятеркой, а затем с четверкой.

Таким образом, в процессе Сортировки вставками элемент записанный в buff “просеивается” к началу массива. А в случаях, когда будет найден элемент со значением меньше чем buff или будет достигнуто начало последовательности – просеивание останавливается.

Хорошая визуальная иллюстрация алгоритма Сортировка вставками есть на википедии:

Затраты времени на работу данного алгоритма полностью зависят от начальных данных: количества элементов в массиве и его изначальной упорядоченности. Это понятно, что чем больше массив – тем больше времени надо на его обработку. Также больше времени потребуется на сортировку массива в котором значения абсолютно не упорядочены.

Алгоритм Сортировка вставками хорош для небольших массивов (до нескольких десятков элементов). Еще эффективнее работает, если данные такого массива ранее были частично отсортированы. Если в массив будут добавляться новые данные (новые элементы), алгоритм сможет их сортировать по мере их добавления (в отличии от сортировки пузырьком и сортировки выбором). Эффективность алгоритма значительно возрастет, если добавить в код алгоритм бинарного поиска.

Предлагаем также посмотреть короткий видоурок по информатике с разбором алгоритма Сортировка вставками:

6 thoughts on “Сортировка вставками”

remenergo.pro:
10.03.2016 в 22:32
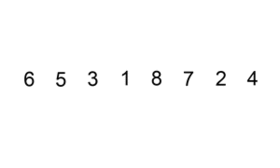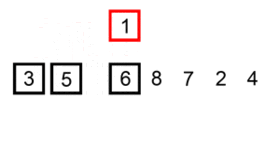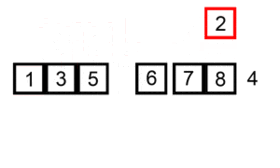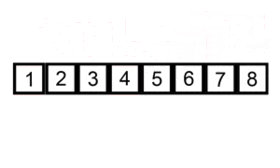
Измените сортировки, чтобы они выводили количество раз, которое выполнились внешний и внутренние циклы.
Ответить
1. Olej:
  12.03.2016 в 18:02
  А зачем? В этой сортировке это и так легко посчитать – общее число 2-х циклов = N * (N-1) / 2 … и не нужно ничего выводить.
  Но вычислительную сложность сортировок (любых) меряют не какими-то повторениями циклов, а оценивают степенью роста числа операций сравнений и перестановок от длины N. И это заранее известно, что плохие сортировки (пузырьковая, вставками … и почти все другие) имеют степень сложности O(N)=N*N (квадратичную), а хорошие (быстрые рекурсивные) – O(N)=N*log(N).
  Ответить
alex:
20.08.2019 в 17:41
Помилка в 21 рядку // a[j + 1] = buff; // повинно бути a[j] = buff;
Ответить
1. Дмитро:
  05.05.2022 в 21:38
  
  В таком случае оно их не изменяет, а в конце выведет что-то вроде 12 12 12 12 12 24 45 45 96 96
  
  Ответить
Maniacal:
01.07.2022 в 12:51
У вас ошибка в коде.
В строке 21.
должно быть не
a[j + 1] = buff;
а
a[j] = buff;
Ответить
Maniacal:
01.07.2022 в 12:58
Всё, понял, почему оно работает.
for (j = i – 1; j >= 0 && a[j] > buff; j–) a[j + 1] = a[j];
a[j + 1] = buff; // и поставим запомненный на его новое место
}
Вот так понятно, а то кажется, что
for (j = i – 1; j >= 0 && a[j] > buff; j–)
{
a[j + 1] = a[j];
a[j + 1] = buff; // и поставим запомненный на его новое место
}
Ответить