Простое возведение числа в степень N – это N – 1 умножений в цикле. А умножение – это дорогая, трудоёмкая операция…
Формулировка данной задачи такая:
- написать функцию возведение в степень X**N, но так, чтобы для этого требовалось минимальное число операций умножения);
- постарайтесь контролировать и включить в вывод число потребовавшихся для вычисления умножений.
P.S. логика такого решения не моя, а знаменитого гуру Чарльза Энтони Хоара (Charles Anthony Richard Hoare), я только записал кодом его решение:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include <assert.h> #include <iostream> using namespace std; double power(double a, int n, int& m) { assert(n > 0 || (a != 0.0 || n != 0)); switch (n) { case 0: return 1; case 1: return a; default: { double a2 = power(a, n / 2, m); if (n & 1) { m += 2; return a * a2 * a2; } else { m++; return a2 * a2; } } } } int main() { setlocale(LC_ALL, "rus"); double e, r; int n, m; while (true) { cout << "что возводить? : "; cin >> e; cout << "в какую степень? : "; cin >> n; m = 0; r = power(e, n, m); cout << e << "**" << n << "=" << r << ", число умножений " << m << endl << endl; } return 0; } |
И вот несколько образцов выполнения, то что должно получиться:
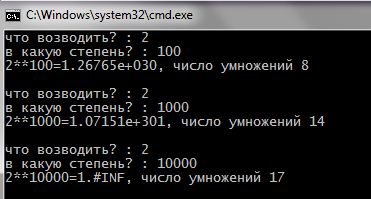
Этот пример ещё раз показывает мощь рекурсии как метода вычислений. Попробуйте записать этот алгоритм в итерационной технике (циклами) … а ещё лучше – объяснить затем кому-то как этот записанный алгоритм работает.
Любите рекурсию!
Для N^15 достаточно 5 умножений. Ваш результат – 6.
И все-таки 6. Пять – это с делением, а эта операция ещё затратнее (если N не степень двойки).