В C любая функция кроме main() может вызывать саму себя. Тобто в тілі функції може бути розміщений виклик цієї ж функції. Це називається рекурсією.
Коли програма виконує код рекурсивної функції– она будет выполнять его бесконечно, если не предусмотреть условие выхода из рекурсии. Об этом надо помнить, чтобы избежать зацикливания вызовов. Поэтому в определении рекурсивной функции обязательно надо указывать условие выхода. Наприклад, можна розмістити її виклик всередині блоку if.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(9); return 0; } |
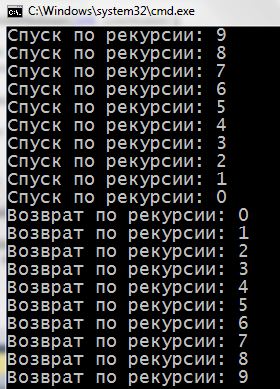
У цій програмі функціяrecursionGoDown() будет вызывать саму себя, поки в неї передається число більше нуля. Каждый раз, функция получает число, от которого в сигнатуре отнимается единица. Как только условие станет ложным (число станет меньше нуля) – вызовы остановятся и начнется выход из рекурсии.
Если мы передаем в такую функцию число 9, викликів буде 10. Програма як би поглиблюється на 10 уровней, выполняя рекурсию. Щоб їй вийти з рекурсії, треба пройти ці десять рівнів назад. Так строка кода
1 | cout << "Возврат по рекурсии: " << someNumber << endl; |
будет выполняться тоже 10 раз, але значенняsomeNumberбудет меняться в обратном порядке. Сначала оно будет соответствовать тому, що передалося в функцію на 10 рівні рекурсії, потом тому что передалось на 9 уровне и т.д.
Хочу обратить внимание на важный момент. При каждом рекурсивном вызове создается новая переменная someNumber с новым значением. Ці змінні будуть займати якесь місце в оперативній пам'яті. якщо викликів 10, как в нашем примере, то и в памяти будет храниться 10 переменных с разными значениями. Можна дописати в програму виведення на екран адрес, по которым хранятся эти значения и убедиться в этом:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(2); return 0; } |
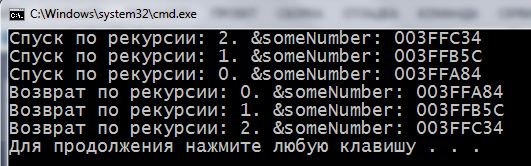
Передаем в функцию число 2: recursionGoDown(2); Рівнів рекурсії буде 3.
Как видно, каждое значение переменной someNumber зберігається в окремому відрізку пам'яті. Во время обратного выхода по рекурсии значения берутся из тех же адресов но в обратном порядке.
Практически каждую поставленную задачу, которую можно решить используя рекурсию, можно реализовать используя итерации циклов. Адже ви легко можете показати на екран числа від 9 до 0 и от 0 до 9 применив циклы. Крім цього слід знати, що рекурсія займе більше пам'яті і буде робити обчислення повільніше, чем итерация.
Але, как утверждают опытные программисты и многие авторы книг, это не значит, что рекурсия бесполезна. Есть задачи, решать которые, используя итерации циклов, сложно и громоздко. А рекурсивне рішення виглядає краще. Для початкового рівня, пока вы изучаете только основы программирования на C , вам достаточно просто понимать, что из себя представляет рекурсия и как она работает.
Подивіться ще відео по темі Рекурсія:
Ви занадто суворі до рекурсії ;-)
1. рекурсія – це загальний математичний апарат, яким теоретично виражаються все обчислюваності алгоритми (це я взяв з мат. теорії алгоритмів).
2. Всі завдання над динамічними структурами даних (списки, черги, дерева, графи, …) вирішуються рекурсивно простіше, а головне наочніше, ніж ітераційно (ітераційні циклічні алгоритми краще працюють над масивами – статичними конструкціями).
3. є алгоритми, які виражаються в 2-3 рядки рекурсивно, але які вкрай складно виписати без рекурсії. Найгарніший приклад того: знаменита завдання “Ханойська вежа”. Багато алгоритми сортування (тих же масивів) краще виражаються в рекурсивної формі.
Рекурсія тільки здається складною, тому що їй не вчать у вітчизняній практиці і не вміють її застосовувати. А в університетах Франції, например, навчання 1-го семестру починають з навчання рекурсивним алгоритмам.
Завжди добре, коли хтось висловлює свою точку зору і свою особисту думку, засноване на досвіді. Початківцям корисно буде почитати.
Як ви пропонуєте використовувати рекурсію в списках і чергах?
рекурсія – це найприродніший спосіб обробки будь-яких динамічних структур (списків, дерев і т.д.), це демонструють функціональні мови програмування, такі як Lisp. Такий підхід набагато ефективніше, ніж ітераційний (циклами). Але це потрібно показувати на прикладах коду…
А простий і красивий приклад рекурсії подивіться в завданні піднесення числа до степеня: https://purecodecpp.com/archives/2734
Вітаю.
Поясніть будь ласка наступні моменти, всю голову зламав, не можу зрозуміти:
1. Якщо в масив в процесі ділення на подмассіви не триває рівно на 2, то програма припинить роботу? Адже в int middle = arr[(L + R)]/2 , де (L + R)/2- ціле число.
2. Якщо в масиві є повторювані числа, і у опорного елемента буде таке ж число, як у числа ліворуч або праворуч, например 1,2,3, 5, 6,5,7
те, не вийде що після того, як програма визначила центральний елемент = 5, і початку його порівняння з елементами правого подмассіва , вона дійшовши до однакового елементу arr [5]= 5 подумає що досягла центрального елемента , перестане порівнювати більш ранні елементи (arr [4}, arr [3]) з центральним, прийме цей 5 елемент за центральний, і далі буде вважати його крайній лівій кордоном?
3. У прикладі розглядалася попарно зміна (зліва і праворуч від центрального) элементов, НЕ удовлеторяющіх умові:
while (середній>arr [i]) i ;
while (середній<arr [j]) j–;
if (i<= у)
{
своп (arr [i], arr [j]);
i ;
j–;
}
А що якщо або спочатку, або після процесу сортування залишився 1
підлягає заміні елемент, например:
1, 2, 3, 8, 5, 6, 7, 9,10
то якщо я правильно зрозумів, він зміниться з центральним елементом,
т.е. вийде 1,2,3,5, 8, 6,7,9,10 ?
4.
Значення центрального елемента може зміниться. У той же час після такої зміни центрального елемента, порівняння, вироблені з більш раннім центральним елементом виявляться невірними, т.к вони не переглядаються, і продовжують йти далі. В результаті сортування виявиться невірною.
Наприклад:
вихідний масив: 1,2,6,9, 4, 10,11,3, 12 з центральним елементом 4.
Після першої заміни (6 на 3) виходить: 1,2,3,9, 4, 10,11,6,12.
Після другої заміни (9 на 4) виходить: 1,2,3,4, 9, 10,11,6,12 і сортування цієї множини закінчуватись. Однак елемент правого підмножини 6 відсортований неправильно.
цікаво, я освоїв рекурсию і ось почав уже вирішувати завдання на цю тему з сайту acmp.ru, і ось на таку задачу натрапив:
сума кубів
(Час: 1 сек. пам'ять: 16 Мб Складність: 52%)
відомо, що будь-яке натуральне число можна представити у вигляді суми не більше ніж чотирьох квадратів натуральних чисел. Вася вирішив придумати аналогічне твердження для кубів – він хоче дізнатися, скільки кубів достатньо для представлення будь-якого числа. Його перша робоча гіпотеза – вісім.
з'ясувалося, що майже всі числа, які Вася зміг придумати, представляються у вигляді суми не більше ніж восьми кубів. Однак число 239, например, не допускає такого уявлення. Тепер Вася хоче знайти будь-які інші такі числа, а также, возможно, якусь закономірність в уявленнях всіх інших чисел, щоб висунути гіпотезу щодо виду всіх чисел, які не подаються у вигляді суми восьми кубів.
Допоможіть Васі написати програму, яка перевіряла б, чи можливо подати цей натуральне число у вигляді суми не більше ніж восьми кубів натуральних чисел, і якщо це можливо, то знаходила б якесь таке уявлення.
Вхідні дані
У вхідному файлі INPUT.TXT записано натуральне число N (1 ≤ N ≤ 2 × 109).
Вихідні дані
У вихідний файл OUTPUT.TXT виведіть не більше восьми натуральних чисел в порядку незростання, куби яких в сумі дають N. Якщо варіантів декілька, то виведіть будь. Якщо шуканого уявлення не існує, то в вихідний файл необхідно вивести слово IMPOSSIBLE.
приклади
№ ВХІД.TXT ВИХІД.TXT
1 17 2 2 1
2 239 НЕМОЖЛИВО
Думав що дп і навіть код написав, а пізніше зрозумів що вектора такого розміру просто не існує, будь ласка допоможіть вирішити це завдання
Не зрозуміло, чому рекурсія починає видавати значення у зворотному порядку, у коді нічого такого не видно:
void recursionGoDown(int someNumber)
{
cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber < 0)
{
recursionGoDown(someNumber – 1); // рекурсивный вызов
}
cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl;
}
По ідеї, як тільки someNumber стає рівним 0, умова оператора if стає хибним і блок {recursionGoDown(someNumber – 1);} має просто ігноруватися. Але натомість він виконується у зворотному порядку. Як це лайно влаштовано???
Qht9a9
0kobwr