Ми з вами вже розібралися з алгоритмом линейного поиска. В той же статье упоминалось, що це не єдиний алгоритм, який дає можливість знайти задане значення в масиві. Существуют другие алгоритмы поиска. Двоичный (бинарный) поиск является более эффективным (проверяется асимптотическим анализом алгоритмов) решением в случае, якщо масив заздалегідь відсортований.
Предположим, что массив из 12-ти элементов отсортирован по возрастанию:
Пользователь задает искомое значение (ключ поиска). Допустим 4. На першій ітерації массив делится на две части (ищем средний элемент – midd): (0 + 11) / 2 = 5 (0.5 отбрасываются). Сначала, перевіряється значення середнього елемента масиву. Якщо воно збігається з ключем – алгоритм прекратит работу и программа выведет сообщение, что значение найдено. В нашем случае, ключ не совпадает со значением среднего элемента.
Если ключ меньше значения среднего элемента, алгоритм не проводитиме пошук в тій половині масиву, которая содержит значения больше ключа (т.е. від середнього елемента до кінця масиву). Правая граница поиска сместится (midd – 1). Далі знову поділ масиву на 2.
Ключ снова не равен среднему элементу. Он больше него. Теперь левая граница поиска сместится (midd + 1).
На третьей итерации средний элемент – это ячейка с индексом 3: (3 + 4) / 2 = 3. Он равен ключу. Алгоритм завершает работу.
Приклад:
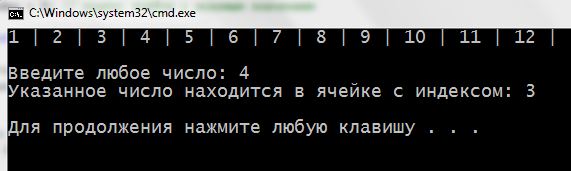
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | #include <iostream> using namespace std; // функция с алгоритмом двоичного поиска int Search_Binary (int arr[], int left, int right, int key) { int midd = 0; while (1) { midd = (left + right) / 2; if (key < arr[midd]) // если искомое меньше значения в ячейке right = midd - 1; // смещаем правую границу поиска else if (key > arr[midd]) // если искомое больше значения в ячейке left = midd + 1; // смещаем левую границу поиска else // иначе (значения равны) return midd; // функция возвращает индекс ячейки if (left > right) // если границы сомкнулись return -1; } } int main() { setlocale (LC_ALL, "rus"); const int SIZE = 12; int array[SIZE] = {}; int key = 0; int index = 0; // индекс ячейки с искомым значением for (int i = 0; i < SIZE; i++) // заполняем и показываем массив { array[i] = i + 1; cout << array[i] << " | "; } cout << "\n\nВведите любое число: "; cin >> key; index = Search_Binary (array, 0, SIZE, key); if (index >= 0) cout << "Указанное число находится в ячейке с индексом: " << index << "\n\n"; else cout << "В массиве нет такого числа!\n\n"; return 0; } |
Результат:
Двоичный поиск является эффективным алгоритмом — его оценка сложности O(log2(n)), в то время как у обычного последовательного поиска O(n). Это значит, что например, для массива из 1024 элементов линейный поиск в худшем случае (когда искомого элемента нет в массиве) обработает все 1024 элемента, но бинарным поиском достаточно обработать log2(1024) = 10 элементов. Такой результат достигается за счет того, що після першого кроку циклу область пошуку звужується до 512 элементов, после второго – до 256 і т.д.
Недостатками такого алгоритма является требование упорядоченности данных, а также возможности доступа к любому элементу данных за постоянное (не зависящее от количества данных) время. Таким образом алгоритм не может работать на неупорядоченных массивах и любых структурах данных, построенных на базе связных списков.
подивіться також, як реалізується алгоритм двійкового пошуку на Сі.




Спасибо. Дуже детально і зрозуміло зовсім початківцю….
У прикладі коду помилка, якщо ввести, например, число 13, то остання ітерація буде вже за кордоном масиву(midd = 12). Програма не падає і дає вірний результат, тому що за кордоном масиву є пам'ять доступна процесу.
int midd = 0;
while (1)
{
if(midd <= п)
{
midd = (left + right) / 2;
if (ключ обр[midd]) // якщо шукане більше значення в осередку
{
вліво = Midd + 1; // зміщуємо ліву межу пошуку
}else // иначе (значения равны)
{
cout<<"key[ "<<midd<<" ] = "<<key<<endl;
return midd; // функція повертає індекс осередки
}
}
} return -1;
}
виправив, начебто, якщо не важко перевір
if(midd <= п)
n — це що?
n - це що? це ваше значення яке ви шукайте в масиві
Наприклад масив з 20 чисел
Чому я вводжу в пошуку n-ну кількість
Мені показує індекс до нього?
Тому що в c ++ індексація нульова (тобто перший елемент для людини – це нульовий елемент для мови, другий елемент для людини – це перший елемент для мови і т.д.)
Все норм, Все норм, Все норм “Указанное число находится в ячейке с индексом: …” Все норм 2, Все норм 3, Все норм, а не з одиниці