взагалі, треба зізнатися, що тема ієрархічних структур досить широка. Про неї можна сперечатися багато і довго, і так і не прийти до спільного знаменника, чітко показуючи що таке ієрархія і як з нею працювати, по яким канонам в сенсі. Я не буду вдаватися в жахливі нетрі математичного Тартар. Це нікому крім академіків не цікаво, і в практичному осяжному занадто тонко.
Итак. Як приклад дерева візьмемо двоичное дерево. Що таке дерево взагалі? Це якийсь набір даних, які вказують на інші дані. динамічний список. До речі списки це приватний вид дерева. причому довічного.
Дерево складається з гілок (вузлів) і листя (элементов). листя – це вузли, які не вказують ні на кого, у них немає гілочок. бінарне дерево – це дерево, в якому у гілки може бути не більше двох листя або гілок. Звідси і його назва – “бінарне” значить “двоичное”, т.е. елементів два або менше. Але ніяк не більше двох.
У звичайного дерева вузлів у гілок більше може бути.
Не буду вдаватися в класифікації дерев. Це теж великий обсяг інформації. Про це можна почитати у Вікіпедії, які вони бувають. Можна набрати в пошуку слово “Граф” і почитати. Головне не наштовхнутися на справжнього графа, у якого бувають графині. Щочетверга та щосуботи :)
Основне правило формування бінарного дерева в С ++: Якщо значення вузла більше додається – додається гілка справа, інакше створюється гілка зліва.
правило просте, від нього і будемо відштовхуватися. Для цього нам знадобиться структура, описувана зразок динамічного списку: Поле даних і два покажчика на праву і ліву гілки. У динамічних списках два покажчика зазвичай пов'язують наступний і попередній елементи, у випадку з деревом цього не знадобиться, оскільки, як правило, прохід по дереву йде з кореня. Хоча звичайно ж може бути і зворотний зв'язок, якщо дуже захочеться.
1 2 3 4 5 6 | struct Branch { char Data; Branch *LeftBranch; Branch *RightBranch; }; |
поле дані представляє дані, на підставі яких будується дерево. Точнее один из элементов данных. Поля філія описують ліву і праву гілки дерева, і є покажчиками на таку ж структуру.
Елементами дерева можуть бути будь-які значення. Массивы, строки (рядок це масив символів якщо що), інші дерева… Полів з даними може бути безліч. На кожне поле можна будувати своє дерево. Цей приклад буде з масивом символів – рядком.
Відразу покажу основний код побудови дерева, щоб можна було зрозуміти що за джерело даних узятий в якості прикладу:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | int main() { Branch *Root = 0; char s[] = "12384562789"; for (int i = 0; s[i]; i++) { Add(s[i], Root); } print(Root); FreeTree(Root); cin.get(); return 0; } |
Строка. Звичайна рядок Сі, яку будемо розводити по гілках. Вузли та листи будуть містити символи, за кодами символів будемо ж визначати вправо або вліво будувати дерево. Хоч я і взяв в рядок цифрові символи, це не важливо. З таким же успіхом можна написати туди рядок “Вони вбили Кенні”.
Як повинна працювати програма? візьмемо символи “12384” з рядка. Спочатку програма бачить , що дерево без коріння. Його ще нема. Потрібно посіяти насіння, щоб воно виросло. Перший символ відповідно стане коренем. другий символ – “2” буде порівнюватися з коренем. За кодом його значення більше. Значить у кореня має зрости гілка вправо (RightBranch) в нашем случае. Далі йде трійка. У нас вже є дві гілки. Програма повинна пройтися по ним, перевірити: 3 больше 1? – Да. піти вправо. є пара. 3 больше 2? Так точно. Після двійки немає гілок, значить потрібно створити гілку вправо для вузла “2”.
Далі йде вісім. Що з ним робити? Теж саме. Від одиниці пройти через двійку до трійки і так же відростити гілку право.
Після вісімки йде 4. Це значення пройде корінь. Оскільки воно більше, програма повинна подивитися, чи є у кореня гілка справа. Есть – піти по ній. пройти “2” і “3”, бо 4 більше за значенням. Далі справа зустрінеться число 8. воно менше. значить “4” вже піде від вісімки не має права, а вліво.
Найпростіший код побудови дерева (з ієрархічною структурою) буде виглядати так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void Add(int aData, Branch *&aBranch) { if (!aBranch) { aBranch = new Branch; aBranch->Data = aData; aBranch->LeftBranch = 0; aBranch->RightBranch = 0; return; } if (aBranch->Data>aData) { Add(aData, aBranch->LeftBranch); } else { Add(aData, aBranch->RightBranch); }; } |
Зверніть увагу: У функції три основні умови:
- Якщо вузол-гілка не створена – створити його, наповнити даними і вказати NULL (0) для його гілок;
- Якщо дані, що передаються більше ніж дані поточного вузла – спробувати побудувати його праву гілку, або якщо вона вже є просто пройти по ній;
- Те ж саме для лівої гілки, якщо дані менше за значенням.
Ієрархія дуже дружить з ryekursiyei. Рекурсивно викликати функції, щоб пройтися по графу, дереву або іншого виду ієрархічної структури – це найпростіший спосіб. Застосовується до речі в штучному інтелекті. Представлений вище код проводить свого роду пошук, але не для видачі результату, а щоб знайти містечко для елемента.
Все! А чого ви думали? древо готове. Иггдрасиль знаменитий цілком міг бути створений ось такими ось 14-ю рядками на С ++. Або який там божественно-космічний мову застосовувався? Якщо ви думаєте, що посадити дерево складно – ось вам очевидне неймовірне. Нет. Нічого складного немає. Ну може бути N-мірне дерево буде трохи більше складніше в реалізації…
В даному випадку щоб зрозуміти принцип його побудови не потрібні тонни коду. Не обов'язково розглядати вставку між вузлами, щоб наприклад впорядкувати дерево або розробляти код для балансування дерева.
Принцип в своїй Naked суті дуже простий. І якщо під час написання якогось павука для серфінгу по сайтах в інтернеті або різних 3D дизайнерських програм типу тих, що розробляють Autodesk, знання дерев і графів потрібні шалені, то в разі простою базової основи досить і чогось простіше.
Залишилося мабуть для дотримання “феншуя” написати код обходу дерева і виведення на екран
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | void print(Branch *aBranch) { if (!aBranch) return; tabs++; print(aBranch->LeftBranch); for (int i = 0; i < tabs; i++) cout << " "; cout << aBranch->Data << endl; print(aBranch->RightBranch); tabs--; return; } |
і звільнення дерева:
1 2 3 4 5 6 7 8 | void FreeTree(Branch *aBranch) { if (!aBranch) return; FreeTree(aBranch->LeftBranch); FreeTree(aBranch->RightBranch); delete aBranch; return; } |
Ось тут мабуть видно ще один принцип роботи з деревами. В друк() рекурсивно викликається поспіль перехід по гілках. Причому між викликами вставлений висновок даних вузла, з якого ростуть гілки, щоб правильно відобразити на екрані або просто відпрацювати скажімо при пошуку даних.
У звільненні так само відбувається рекурсивний виклик звільнення гілок. Спочатку всю ліву, потім всю праву з їх подветкой і листами, і тільки потім звільняється сам викликає вузол. Це важливо, оскільки якщо поставити delete на початку функції отримаємо або помилку (що швидше за все) або все зростаючі гілки з вузла просто не зможуть звільнитися, зависнувши в пам'яті сміттям.
Про всяк випадок поясню ще один фінт у висновку:
1 2 | for (int i = 0; i < tabs; i++) cout << " "; cout << aBranch->Data << endl; |
Перед виведенням даних поточного вузла виводимо кілька відступів. Зроблено це для краси, щоб на екрані виглядало як справжнє дерево, а не просто набір даних. Щоб можна було побачити структуру на власні очі.
Для цього визначаємоглобальну змінну int вкладки=0; яка буде рахувати кількість відступів, і за фактом (до речі!) бути носієм значення рівня вузла, т.е. номером його вкладеності. Скільки у цього вузла батьків-гілок аж до кореня. Це поняття теж можна зустріти в літературі про дерева. Так що воно там (в коді мається на увазі) не тільки для наведення краси на екрані.
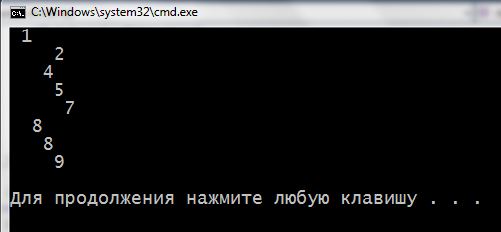
Ось повний код (при запуску дерево “росте” не зверху вниз, як на малюнках, а зліва направо. Не хотілося ускладнювати код):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | #include <iostream> using namespace std; int tabs = 0; //Для создания отступов //Кол-во отступов высчитывается по кол-ву рекурсивного вхождения при выводе в фукцию print //Структура ветки struct Branch { char Data; //Поле данных Branch *LeftBranch; //УКАЗАТЕЛИ на соседние веточки Branch *RightBranch; }; //Функция внесения данных void Add(char aData, Branch *&aBranch) { //Если ветки не существует if (!aBranch) { //создадим ее и зададим в нее данные aBranch = new Branch; aBranch->Data = aData; aBranch->LeftBranch = 0; aBranch->RightBranch = 0; return; } else //Иначе сверим вносимое if (aBranch->Data>aData) { //Если оно меньше того, что в этой ветке - добавим влево Add(aData, aBranch->LeftBranch); } else { //Иначе в ветку справа Add(aData, aBranch->RightBranch); }; } //Функция вывода дерева void print(Branch *aBranch) { if (!aBranch) return; //Если ветки не существует - выходим. Выводить нечего tabs++; //Иначе увеличим счетчик рекурсивно вызванных процедур //Который будет считать нам отступы для красивого вывода print(aBranch->LeftBranch); //Выведем ветку и ее подветки слева for (int i = 0; i<tabs; i++) cout << " "; //Потом отступы cout << aBranch->Data << endl; //Данные этой ветки print(aBranch->RightBranch);//И ветки, что справа tabs--; //После уменьшим кол-во отступов return; } void FreeTree(Branch *aBranch) { if (!aBranch) return; FreeTree(aBranch->LeftBranch); FreeTree(aBranch->RightBranch); delete aBranch; return; } int main() { Branch *Root = 0; char s[] = "18452789"; for (int i = 0; s[i]; i++) { Add(s[i], Root); } print(Root); FreeTree(Root); cin.get(); return 0; } |
На экране:
Що ж… Мабуть на цьому про бінарні дерева в С ++ все. Як ще коротше описати принципи я не знаю, але абсолютно впевнений, що лізти в нетрі академічних просторів (читай: прострації) не варто. Чим простіше виглядає пояснення, тим воно ближче до правди.
Відео. Автор – “mycodeschool”:
При всій повазі, стаття ниочем. бінарні дерева – не обов'язково дерева пошуку. Тому “Основне правило формування бінарного дерева в С ++” не канал.
Процес видалення вузла з дерева не описаний. Збалансовані дерева теж (згадати хоча б коштувало).
Спасибо! Мені дуже допомагає, просто написано і зрозуміло. Вчуся по Вашому сайту
Спасибо! для новаків, те що потрібно.
Те що треба!
Дякуємо за виведення дерева, довго шукав