решето Ератосфена – один з найдавніших алгоритмів, дозволяють знайти числа, які називають “простими”. Тобто,. числа, які можуть ділитися без залишку тільки на одиницю і на себе. наприклад число 2. На що з натуральних (цілих) чисел можна розділити 2, щоб не отримувати залишок? Тільки на 2 і на 1. або число 7. Теж саме. Без залишку воно ділиться знову таки тільки на себе і одиницю.
Досить простий алгоритм ще до нашої ери придумав хитрий дядько Ератосфен Киренский. Грек за національністю. математика, астроном, географ. Решето дядьки Ератосфена досить популярний алгоритм пошуку.
Якогось особливого опису цей алгоритм насправді не вимагає. Він передбачає два циклу проходу по набору чисел. Перший визначає наступне просте число, второй вкладений в нього викреслює всі складні числа (за певною формулою) стоять після цього простого. Треба відразу обмовитися, що другий цикл відразу всі складні цифри не викреслює.
Він викреслює наступні числа після простого, які від цього простого знаходяться на певній відстані. Відстань це розраховується за формулою: Поточний елемент в квадраті + значення цього елемента.
Наприклад якщо число 5 просте, то наступне після нього, яке стоїть викреслити дорівнюватиме 5*5 = 10, потім 5*5+5 = 15, потім 5*5+5+5 = 20… і так далі. Викреслюються таким чином числа кратні цьому знайденому простому. Знаходження простого починається з числа 2. відповідно викреслюються 2*2, 2*2+2, 2*2+2+2…
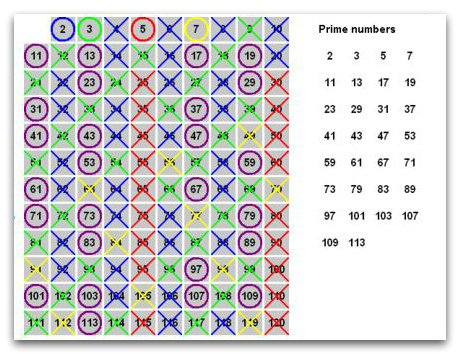
Гарна ілюстрація є на сайті Вікіпедії:
Беремо Перший простий число 2 (синій кружечок) і викреслюємо всі числа, які кратні двом (сині хрестики). Потім беремо просте число 3 (зелений кружечок) і викреслюємо всі що йому кратно (зелені хрестики) і т.д.
Після того, як числа викреслені зі списку легко визначити наступне просте число – воно буде першим не викреслене після поточного.
Оскільки сам код не дуже то і великий, я не буду розбивати його на блоки, там нічого то і конкретизувати. Виглядає він приміром так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | #include <iostream> using namespace std; int main() { int n = 100; //Считать числа до этого //Запрашиваем массив int *a = new int[n + 1]; //Наполняем его числами для решета for (int i = 0; i <= n; i++) a[i] = i; //*********************************************************** //Проводим главный цикл. - Начало работы решета for (int i = 2; i * i <= n; i++) { if (a[i]) //Если текущее число не равно 0 - начинаем от него искать сложные for (int j = i*i; j <= n; j += i) //И обнуляем их ячейки, чтобы больше не проверять их в цикле a[j] = 0; } // Решето окончило отсев - в массиве остались только простые //************************************************************ //Выводим необнуленные - простые for (int i = 2; i < n; i++) { if (a[i]) { cout << a[i] << ' '; } } cout << endl << endl; delete[] a; //И освобождаем массив return 0; } |
Працює цей код наступним чином: Запитується масив чисел. Я спеціально для зручності додав до масиву один “допоміжний” елемент в кінець, щоб програма починала працювати з масивом не з нуля, як прийнято відраховувати в С ++ массивы, а з одиниці.
Для наочності природно. Після запиту масив заповнюється числами по порядку. Можна було звичайно не використовувати масив чисел, а просто масив булевих (true, false), і простими числами вважати номера елементів, які після просіювання міститимуть true, але я вирішив, що це не так наочно.
Після того, як числа в масиві розміщені (1,2,3,4,5,6,7,8,9,10…n) можна приступати до їх просівання. Поки що на початковому етапі все числа в решеті вважаються програмою простими. Перша ітерація циклу бере перший (а точніше друге за рахунком) число – 2. Від цього числа другий цикл обнуляє елементи масиву, які потрапляють під фільтр-умова Число * Число + Число.
Таким чином просіваються числа кратні двом після двійки. Далі перший цикл продовжує прохід, перевіряючи умова if(a[i]) , т.е. чи є в осередку число, відрізняється від нуля (ми адже обнуляем складні числа). Як тільки таке число буде знайдено, знову вже від нього спрацює другий цикл, обнуляючи після знайденого кратні йому числа, стоять після нього.
І так цикли просівають числа поки не досягнуть заданої нами кордону просіювання – до якого числа виловлювати прості.
Де використовуються прості числа? Хм… Наприклад в криптографії. Так само в деяких генераторах випадкових чисел. Ну і звичайно ж у ВНЗ :) По суті решетом викладачі теж не гребують і регулярно вміло балують студентів завданнями “Знаходження простого числа”. Ось за допомогою такого решета це завдання цілком вирішувана.

А як реалізувати відкидання на початковому етапі всіх парних чисел крім двійки? Щоб потім вже серед непарних шукати прості?
“5*5 = 10, потім 5*5+5 = 15, потім 5*5+5+5 = 20 ...” виправте!