Сортировка вставками С (відео)

Ще одним алгоритмом, розробленим для упорядкування масивів, є алгоритм Сортування вставками (вставка Сортувати). цей алгоритм(як і інші, розглянуті на нашому сайті) досить простий. Він складається з двох циклів (один вкладений в інший). Перший цикл виробляє прохід по масиву, а другий – переміщення оброблюваних елементів. Давайте відразу подивимося, як може виглядати код такого сортування, а вже нижче розберемо, как он работает.

#include <iostream>
using namespace std;

int main()
{
	const int N = 10;
	int a[N] = { 12, 5, 3, 2, 45, 96, 6, 8, 11, 24 };

	int buff = 0;	// для хранения перемещаемого значения
	int i, j;		// для циклов		

	/************* Начало сортировки *******************/
	for (i = 1; i < N; i++)
	{
		buff = a[i]; // запомним обрабатываемый элемент
		// и начнем перемещение элементов слева от него
		// пока запомненный не окажется меньше чем перемещаемый
		for (j = i - 1; j >= 0 && a[j] > buff; j--)
					a[j + 1] = a[j];	

		a[j + 1] = buff; // и поставим запомненный на его новое место	
	}
	/************* Конец сортировки *******************/

	for (int i = 0; i < N; i++) // вывод отсортированного массива
		cout << a[i] << '\t';
	cout << endl;
}

#include <iostream>

using namespace std;

int main()

{

const int N = 10;

int a[N] = { 12, 5, 3, 2, 45, 96, 6, 8, 11, 24 };

int buff = 0; // для хранения перемещаемого значения

int i, j; // для циклов

/************* Начало сортировки *******************/

for (i = 1; i < N; i++)

{

buff = a[i]; // запомним обрабатываемый элемент

// и начнем перемещение элементов слева от него

// пока запомненный не окажется меньше чем перемещаемый

for (j = i - 1; j >= 0 && a[j] > buff; j--)

a[j + 1] = a[j];

a[j + 1] = buff; // и поставим запомненный на его новое место

}

/************* Конец сортировки *******************/

for (int i = 0; i < N; i++) // вывод отсортированного массива

cout << a[i] << '\t';

cout << endl;

}

алгоритм Сортування вставками можна описати наступними позиціями:

Запам'ятати на тимчасову змінну ( любитель в прикладі) значення поточного елемента масиву;
Поки елементи зліва від того, що запам'ятав значення більше ніж запомненное – переміщаємо їх на позицію вправо. Получается, що попередній елемент займе осередок запомненного. А тот, що стоїть перед попереднім – переміститься в свою чергу на місце попереднього. І так елементи будуть рухатися один за одним.
Рух елементів закінчується, якщо черговий елемент, який потрібно зрушити, виявляється за значенням менше, ніж той, що запам'ятали в тимчасову змінну на початку циклу.
Цикл бере наступний елемент, і знову зрушує все, які розташовані перед ним і великі за значенням.

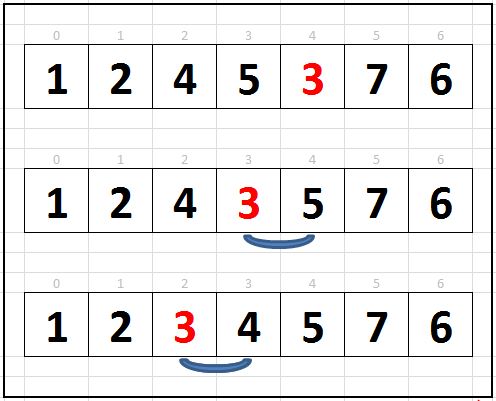
Покажемо візуально переміщення значення в масиві з семи елементів під час роботи сортування вставками:

На першій ітерації в змінну-буфер запишеться значення з комірки з індексом 1 і цикл буде перевіряти цей елемент. Там у нас знаходиться число 2. Воно більше значення, яке записано в нульовий осередку, тому переміщення не буде. Далі в змінну-буфер запишеться значення з комірки з індексом 2 і знову піде порівняння зі значеннями зліва і т.д. Тільки на четвертій ітерації зовнішнього циклу почнеться перезапис значень. Трійка спочатку поміняється місцями з п'ятіркою, а потім з четвіркою.

Таким образом, в процесі сортування вставками елемент записаний в любитель “просівається” до початку масиву. А у випадках, коли буде знайдений елемент із значенням менше ніжлюбитель або буде досягнуто початку послідовності – просіювання зупиняється.

Хороша візуальна ілюстрація алгоритму Сортування вставками є навікіпедії:

Витрати часу на роботу даного алгоритму повністю залежать від початкових даних: кількості елементів в масиві і його початкової впорядкованості. Це зрозуміло, що чим більше масив – тим більше часу треба на його обробку. Також більше часу буде потрібно на сортування масиву в якому значення абсолютно не впорядковані.

алгоритм Сортування вставками хороший для невеликих масивів (до декількох десятків елементів). Ще ефективніше працює, якщо дані такого масиву раніше були частково відсортовані. Якщо в масив будуть додаватися нові дані (нові елементи), алгоритм зможе їх сортувати по мірі їх додавання (на відміну від сортування бульбашкою і сортування вибором). Ефективність алгоритму значно зросте, якщо додати в код алгоритм бінарного пошуку.

Пропонуємо також подивитися короткий відоурок з інформатики з розбором алгоритму Сортування вставками:

6 думки про "Сортування вставками”

remenergo.pro говорить:
10.03.2016 at 22:32
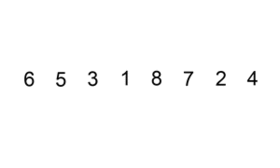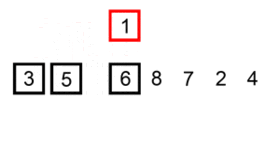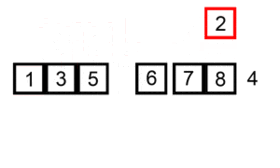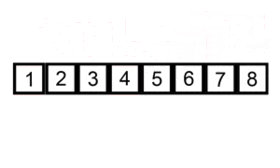
змініть сортування, щоб вони виводили кількість разів, яке виконалися зовнішній і внутрішні цикли.
відповісти
1. Olej говорить:
  12.03.2016 at 18:02
  А навіщо? У цій сортуванні це і так легко порахувати – загальне число 2-х циклів = N * (N-1) / 2 … і не потрібно нічого виводити.
  Але обчислювальну складність угруповань (будь-яких) міряють не якимись повтореннями циклів, а оцінюють ступенем зростання числа операцій порівнянь і перестановок від довжини N. І це заздалегідь відомо, що погані сортування (пузырьковая, вставками … і майже всі інші) мають ступінь складності O(N)N * = N (квадратичную), а хороші (швидкі рекурсивні) – O(N)= N * журналу(N).
  відповісти
Алекс говорить:
20.08.2019 at 17:41
Помилка в 21 рядку // a[j + 1] = buff; // повинно бути a[j] = buff;
відповісти
1. Дмитро говорить:
  05.05.2022 at 21:38
  
  В такому випадку воно їх не змінює, а в кінці виведе шось на кшталт 12 12 12 12 12 24 45 45 96 96
  
  відповісти
Маніакальний говорить:
01.07.2022 at 12:51
У вас помилка у коді.
В рядку 21.
повинно бути не
a[j + 1] = buff;
а
a[j] = buff;
відповісти
Маніакальний говорить:
01.07.2022 at 12:58
Усе, зрозумів, чому воно працює.
for (J = я – 1; j >= 0 && a[j] > любитель; j–) a[j + 1] = а[j];
a[j + 1] = buff; // і поставимо запомненний на його нове місце
}
Ось так зрозуміло, а то здається, що
for (J = я – 1; j >= 0 && a[j] > любитель; j–)
{
a[j + 1] = а[j];
a[j + 1] = buff; // і поставимо запомненний на його нове місце
}
відповісти