гіпотеза Коллатц – це одна з невирішених проблем в математиці з 1937 року (гіпотеза Коллатц, Collatz гіпотеза), яку математики не можуть ні довести, ні спростувати. Гіпотеза полягає в тому, для будь-якого натурального числа n>1 послідовне застосування функції:


– приведе до числовому ряду, который, В підсумку (рано чи пізно) приведе до числа 1 (то есть, на кожному кроці перетворень для парних значень наступним кроком обчислюється n / 2, а для непарних – 3п + 1). Наприклад, для n = 3 це буде ряд перетворень: 3,10,5,16,8,4,2,1. Для деяких n ця послідовність чисел буде дуже коротким, але для деяких – дуже довгою…
Наше завдання не в тому, щоб вирішити задачу, яку всі математики світу не можуть вирішити 80 років, а в тому, щоб для будь-якого n побудувати ланцюжок числових для такого перетворення (те, що математики називають: числа-градини).
Конечно, как и раньше, одним із критеріїв якості рішення буде: код повинен бути записаний якомога коротше.
Рішення.
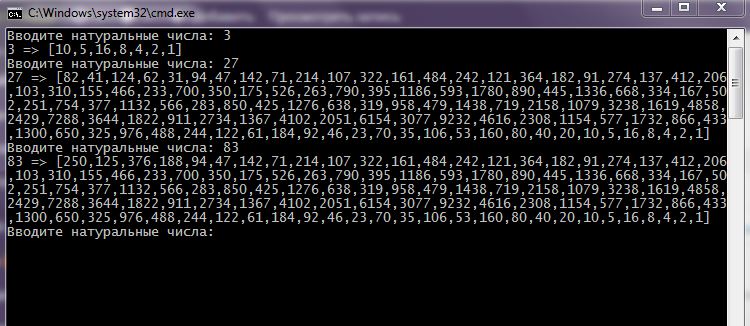
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include <iostream> #include <sstream> using namespace std; // гипотеза Коллатца void collatz( unsigned long val ) { cout << val << " => ["; while( true ) { val = val & 1 ? 3 * val + 1 : val >> 1; cout << val << ( val > 1 ? "," : "]\n" ); if( 1 == val ) return; } } int main() { setlocale(LC_ALL, "rus"); string e; unsigned long d; while( true ) { cout << "Вводите натуральные числа: "; getline( cin, e ); istringstream ist( e ); while( ist >> d ) collatz( d ); } } |
Як це виконується:
#include
using namespace std;
int main() {
setlocale(LC_ALL, “rus”);
довго все = 1;
cin >> всі;
for (;;) {
if (всі % 2 == 0) {
все / = 2;
cout << всі << endl;
}
else {
все = (всі * 3) + 1;
cout << всі << endl;
}
if (все == 1) {
break;
}
}
system("pause");
return 0;
}
Микола, типу у тебе коротше?
Гаразд про перевірку парності і розподіл на 2 розподілом, х з ним.
Але ти б хоч висновок не дублював.