Абсолютно особливу групу алгоритмів складають сортування - сортувати в практиці доводиться найрізноманітніші об'єкти і з найрізноманітніших критеріям. Аналіз алгоритмів сортування добре і докладно вивчено, як жоден інший розділ обчислювальної математики. Основним питанням будь-якого алгоритму сортування є його обчислювальна складність - число операцій порівняння-обміну, необхідних для сортування послідовності довжини N, так зване O( N ).
Неприємним обставиною є те, що для різних алгоритмів розрізняються середня складність (на більшості тестових послідовностей) і максимальна складність (на найгіршою для методу тестової послідовності). Для кількох десятків алгоритмів сортування, пропонованих в процесі навчання програмуванню, показано, що переважна більшість з них (інтуїтивно зрозумілих) є гіршими і в сенсі середньої і в сенсі максимальної складності. Як приклад, популярна у студентів пузырьковая сортировка є найгіршою з усіх взагалі відомих.
ефективними (за складністю) з усього безлічі методів є тільки кілька методів швидких рекурсивних угруповань. Вони то і представлені в реалізаціях алгоритмів STL. Стандарти не наполягають на жорсткому обмеженні на внутрішніх механізмах їх реалізації, тому можуть бути варіанти в залежності від використовуваної бібліотеки.
тепер, володіючи деякими знаннями про алгоритмах, функторах і загалом станом справ з угрупованнями, ми готові розглянути варіанти реалізації всього цього в своєму коді. Для початку ми різноманітними способами сортуємо числові послідовності. приклад Velikon, але він призначений не тільки, і не скільки, для ілюстрації, як для подальшого самостійного експериментування:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | #include <iostream> #include <vector> #include <cmath> #include <algorithm> #include <ctime> using namespace std; vector<unsigned> create( int size, char mode = '-' ) { // заполнить в указанном порядке vector<unsigned> vect = vector<unsigned>( size ); unsigned j = 0; if( '?' == mode ) srand( (unsigned int)time( NULL ) ); for( vector<unsigned>::iterator i = vect.begin(); i != vect.end(); i++ ) switch( mode ) { case '+' : *i = ++j; break; case '?' : *i = nearbyint( (double)rand() / RAND_MAX * ( size - 1 ) ) + 1; break; case '-' : default : *i = size--; break; } return vect; } bool test( vector<unsigned>& v ) { // финальный контроль монотонности bool dir = v[ 0 ] < v[ 1 ]; // порядок сортировки vector<unsigned>::iterator i = v.begin(); while( true ) { auto j = i; if( ++j == v.end() ) break; if( ( *i <= *j ) != dir ) return false; i++; } return true; } typedef void (sort_func)( vector<unsigned>& ); // предварительные объявления функций сортировки: sort_func sort1, sort2, sort3, sort4, sort5, sort6; sort_func* variants[] = { sort1, sort2, sort3, sort4, sort5, sort6 }; ostream& operator <<( ostream& stream, vector<unsigned>& v ) { // отладка-контроль stream << "[ "; for( auto x : v ) stream << x << " "; return stream << "]"; } int main( int argc, char *argv[] ) { if( argc < 3 ) return 1; char *parm = argv[ 1 ]; // длина и порядок тест-последовательности char mode = *parm == '-' || *parm == '+' || *parm == '?' ? *parm++ : '-'; int size = atoi( parm ); if( size <= 0 ) return 2; int debug = 0; parm = argv[ 2 ]; // вариант и уровень отладки while( '+' == *parm ) debug++, parm++; unsigned var = atoi( parm ); if( var > 0 && var <= sizeof( variants ) / sizeof( variants[ 0 ] ) ) var--; else return 3; vector<unsigned> vect = create( size, mode ); if( debug ) cout << vect << endl; variants[ var ]( vect ); if( debug ) cout << vect << endl; else cout << ( test( vect ) ? "OK" : "not OK" ) << endl; } //-------------------------------------------------------------------------------------------- // Быстрая сортировка. Сложность в среднем O( n*log(n) ), но в худшем случае O( n*n ) void sort1( vector<unsigned>& v ) { sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- bool sort_function( unsigned f, unsigned s ) { return f > s; } void sort2( vector<unsigned>& v ) { // использование функции как предикакта sort( v.begin(), v.end(), sort_function ); }; //-------------------------------------------------------------------------------------------- struct sort_class { // функтор сравнения bool operator()( unsigned f, unsigned s ) { return f > s; } }; void sort3( vector<unsigned>& v ) { sort( v.begin(), v.end(), sort_class() ); }; //-------------------------------------------------------------------------------------------- // Сортировка подпоследователности. Гарантированная сложность O( n*log(n) ) в любом случае. // Обычно сортировка в куче выполняется в 2-5 раз медленнее быстрой сортировки sort(). void sort4( vector<unsigned>& v ) { partial_sort( v.begin(), v.end(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка слиянием. Сложность O( n*log(n) ) или O( n*log(n)*log(n) ), если без дополнительной памяти void sort5( vector<unsigned>& v ) { stable_sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка в куче (heap) - вызывают функции, непосредственно работающие с кучей // (то есть с бинарным деревом, используемым в реализации этих алгоритмов). // Сложность O( n+n*log(n) ) void sort6( vector<unsigned>& v ) { make_heap( v.begin(), v.end() ); sort_heap( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- |
Перед компіляцією програми, в MVS натисніть Alt + F7 і внесіть Аргументи команди ?30 +3: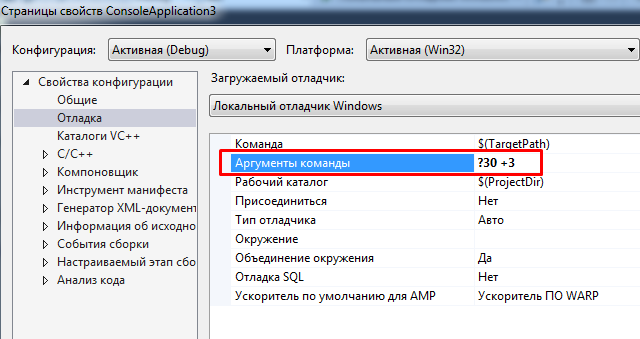
Деяка громіздкість прикладу пов'язана з тим, що ми в одному коді об'єднуємо і всі надані STL алгоритми сортування, і різноманітні тестові сортовані послідовності, например:
кілька випадкових (?) послідовностей довжини 30, сортируемих з використанням (3) функтора порівняння, і деталізованим (+) висновком вхідний і вихідний послідовності:

інверсна (зворотна, спадна) послідовність, сортируемое (6) «В купі» з використанням бінарного дерева (аргументи команди -30 +6 ):

довга (1000000) послідовність, в тих же, що і попередній випадок, умовах, але з висновком тільки діагностики коректності результату (аргументи команди -1000000 6 ):

Бібліотека STL надає 3 групи алгоритмів сортування:
сортувати() – найбільш швидке сортування в середньому ( O( N * журнал( N ) ), але яка може «провалюватися» в гіршому випадку до O( N * N ) (а це дуже поганий показник);
sort_heap() – сортування в «в купі», з використанням бінарного дерева, складність якої завжди не гірше O( N + N * журнал( N ) ) (це гірше сортувати() в середньому, але краще в найгіршому випадку);
stable_sort() – «Стійка» сортування злиттям, стійкість якої означає, що вона зберігає відносний порядок рівних елементів після сортування. Це іноді дуже важливо. Складність цього алгоритму не набагато поступається сортувати();
Використовуйте той алгоритм, який найбільше відповідає обмеженням вашого завдання.