Вообще, надо признаться, что тема иерархических структур весьма широка. О ней можно спорить много и долго, и так и не прийти к общему знаменателю, четко показывающему что такое иерархия и как с ней работать, по каким канонам в смысле. Я не стану вдаваться в ужасные дебри математического Тартара. Это никому кроме академиков не интересно, и в практическом обозримом слишком тонко.
Итак. В качестве примера дерева возьмем двоичное дерево. Что такое дерево вообще? Это некий набор данных, которые указывают на другие данные. Динамический список. Кстати списки это частный вид дерева. Причем двоичного.
Дерево состоит из веток (узлов) и листьев (элементов). Листья – это узлы, которые не указывают ни на кого, у них нет веточек. Бинарное дерево – это дерево, в котором у ветки может быть не более двух листьев или веток. Отсюда и его название – “бинарное” значит “двоичное”, т.е. элементов два или меньше. Но никак не более двух.
У обычного дерева узлов у веток больше может быть.
Не буду вдаваться в классификации деревьев. Это тоже большой объем информации. Об этом можно почитать в Википедии, какие они бывают. Можно набрать в поиске слово “Граф” и почитать. Главное не наткнуться на настоящего графа, у которого бывают графини. По четвергам и субботам :)
Основное правило формирования бинарного дерева в С++: Если значение узла больше добавляемого – добавляется ветка справа, иначе создается ветка слева.
Правило простое, от него и будем отталкиваться. Для этого нам понадобится структура, описываемая наподобие динамического списка: Поле данных и два указателя на правую и левую ветки. В динамических списках два указателя обычно связывают следующий и предыдущий элементы, в случае с деревом этого не понадобится, поскольку, как правило, проход по дереву идет с корня. Хотя конечно же может быть и обратная связь, если очень захочется.
1 2 3 4 5 6 | struct Branch { char Data; Branch *LeftBranch; Branch *RightBranch; }; |
Поле Data представляет данные, на основании которых строится дерево. Точнее один из элементов данных. Поля Branch описывают левую и правую ветки дерева, и являются указателями на такую же структуру.
Элементами дерева могут быть любые значения. Массивы, строки (строка это массив символов если что), другие деревья… Полей с данными может быть множество. На каждое поле можно строить свое дерево. Этот пример будет с массивом символов – строкой.
Сразу покажу основной код построения дерева, чтоб можно было понять что за источник данных взят в качестве примера:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | int main() { Branch *Root = 0; char s[] = "12384562789"; for (int i = 0; s[i]; i++) { Add(s[i], Root); } print(Root); FreeTree(Root); cin.get(); return 0; } |
Строка. Обычная строка Си, которую будем разводить по веткам. Узлы и листы будут содержать символы, по кодам символов будем же определять вправо или влево строить дерево. Хоть я и взял в строку цифровые символы, это не важно. С таким же успехом можно написать туда строку “Они убили Кенни”.
Как должна работать программа? Возьмем символы “12384” из строки. Сначала программа видит , что дерево без корня. Его еще нет. Нужно посеять семя, чтоб оно выросло. Первый символ соответственно станет корнем. Второй символ – “2” будет сравниваться с корнем. По коду его значение больше. Значит у корня должна вырасти ветка вправо (RightBranch) в нашем случае. Далее идет тройка. У нас уже есть две ветки. Программа должна пройтись по ним, проверить: 3 больше 1? – Да. Пойти вправо. Там двойка. 3 больше 2? Так точно. После двойки нет веток, значит нужно создать ветку вправо для узла “2”.
Дальше идет восемь. Что с ним делать? То же самое. От единицы пройти через двойку до тройки и так же отрастить ветку право.
После восьмерки идет 4. Это значение пройдет корень. Поскольку оно больше, программа должна посмотреть, есть ли у корня ветка справа. Есть – пойти по ней. Пройти “2” и “3”, ибо 4 больше по значению. Дальше справа встретится число 8. Оно меньше. Значит “4” уже пойдет от восьмерки не вправо, а влево.
Простейший код построения дерева (с иерархической структурой) будет выглядеть так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void Add(int aData, Branch *&aBranch) { if (!aBranch) { aBranch = new Branch; aBranch->Data = aData; aBranch->LeftBranch = 0; aBranch->RightBranch = 0; return; } if (aBranch->Data>aData) { Add(aData, aBranch->LeftBranch); } else { Add(aData, aBranch->RightBranch); }; } |
Обратите внимание: В функции три основных условия:
- Если узел-ветка не создана – создать его, наполнить данными и указать NULL (0) для его веток;
- Если передаваемые данные больше чем данные текущего узла – попытаться построить его правую ветку, или если она уже есть просто пройти по ней;
- То же самое для левой ветки, если данные меньше по значению.
Иерархия очень дружит с рекурсией. Рекурсивно вызывать функции, чтоб пройтись по графу, дереву или другому виду иерархической структуры – это самый простой способ. Применяется кстати в искусственном интеллекте. Представленный выше код проводит своего рода поиск, но не для выдачи результата, а чтобы найти местечко для элемента.
Все! А чего вы думали? Древо готово. Иггдрасиль знаменитый вполне мог быть создан вот такими вот 14-ю строками на С++. Или какой там божественно-космический язык применялся? Если вы думаете, что посадить дерево сложно – вот вам очевидное невероятное. Нет. Ничего сложного нет. Ну может быть N-мерное дерево будет чуть более сложнее в реализации…
В данном случае чтоб понять принцип его построения не нужны тонны кода. Не обязательно рассматривать вставку между узлами, чтоб к примеру упорядочить дерево или разрабатывать код для балансировки дерева.
Принцип в своей Naked сущности очень прост. И если при написании какого-то паука для серфинга по сайтам в интернете или разных 3D дизайнерских программ типа тех, что разрабатывают Autodesk, знания деревьев и графов нужны сумасшедшие, то в случае простой базовой основы достаточно и чего-то попроще.
Осталось пожалуй для соблюдения “феншуя” написать код обхода дерева и вывода на экран
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | void print(Branch *aBranch) { if (!aBranch) return; tabs++; print(aBranch->LeftBranch); for (int i = 0; i < tabs; i++) cout << " "; cout << aBranch->Data << endl; print(aBranch->RightBranch); tabs--; return; } |
и освобождения дерева:
1 2 3 4 5 6 7 8 | void FreeTree(Branch *aBranch) { if (!aBranch) return; FreeTree(aBranch->LeftBranch); FreeTree(aBranch->RightBranch); delete aBranch; return; } |
Вот здесь пожалуй виден еще один принцип работы с деревьями. В print() рекурсивно вызывается подряд переход по веткам. Причем между вызовами вставлен вывод данных узла, из которого растут ветки, чтоб правильно отобразить на экране или просто отработать скажем при поиске данных.
В освобождении так же происходит рекурсивный вызов освобождения веток. Сначала всю левую, потом всю правую с их подветками и листами, и только потом освобождается сам вызывающий узел. Это важно, поскольку если поставить delete в начале функции получим либо ошибку (что скорее всего) либо все растущие ветки из узла просто не смогут освободиться, зависнув в памяти мусором.
На всякий случай поясню еще один финт в выводе:
1 2 | for (int i = 0; i < tabs; i++) cout << " "; cout << aBranch->Data << endl; |
Перед выводом данных текущего узла выводим некоторое количество отступов. Сделано это для красоты, чтоб на экране выглядело как настоящее дерево, а не просто набор данных. Чтоб можно было увидеть структуру воочию.
Для этого определяем глобальную переменную int tabs=0; которая будет считать количество отступов, и по факту (кстати!) являться носителем значения уровня узла, т.е. номером его вложенности. Сколько у этого узла родителей-веток вплоть до корня. Это понятие тоже можно встретить в литературе про деревья. Так что оно там (в коде имеется ввиду) не только для наведения красоты на экране.
Вот полный код (при запуске дерево “растет” не сверху вниз, как на рисунках, а слева направо. Не хотелось усложнять код):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | #include <iostream> using namespace std; int tabs = 0; //Для создания отступов //Кол-во отступов высчитывается по кол-ву рекурсивного вхождения при выводе в фукцию print //Структура ветки struct Branch { char Data; //Поле данных Branch *LeftBranch; //УКАЗАТЕЛИ на соседние веточки Branch *RightBranch; }; //Функция внесения данных void Add(char aData, Branch *&aBranch) { //Если ветки не существует if (!aBranch) { //создадим ее и зададим в нее данные aBranch = new Branch; aBranch->Data = aData; aBranch->LeftBranch = 0; aBranch->RightBranch = 0; return; } else //Иначе сверим вносимое if (aBranch->Data>aData) { //Если оно меньше того, что в этой ветке - добавим влево Add(aData, aBranch->LeftBranch); } else { //Иначе в ветку справа Add(aData, aBranch->RightBranch); }; } //Функция вывода дерева void print(Branch *aBranch) { if (!aBranch) return; //Если ветки не существует - выходим. Выводить нечего tabs++; //Иначе увеличим счетчик рекурсивно вызванных процедур //Который будет считать нам отступы для красивого вывода print(aBranch->LeftBranch); //Выведем ветку и ее подветки слева for (int i = 0; i<tabs; i++) cout << " "; //Потом отступы cout << aBranch->Data << endl; //Данные этой ветки print(aBranch->RightBranch);//И ветки, что справа tabs--; //После уменьшим кол-во отступов return; } void FreeTree(Branch *aBranch) { if (!aBranch) return; FreeTree(aBranch->LeftBranch); FreeTree(aBranch->RightBranch); delete aBranch; return; } int main() { Branch *Root = 0; char s[] = "18452789"; for (int i = 0; s[i]; i++) { Add(s[i], Root); } print(Root); FreeTree(Root); cin.get(); return 0; } |
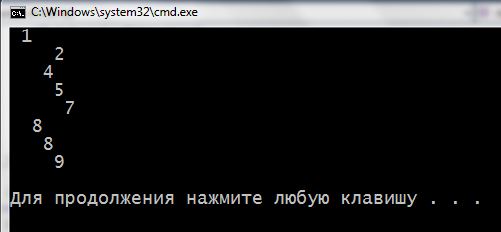
На экране:
Что ж… Пожалуй на этом про бинарные деревья в С++ все. Как еще короче описать принципы я не знаю, но абсолютно уверен, что лезть в дебри академических пространств (читай: простраций) не стоит. Чем проще выглядит объяснение, тем оно ближе к правде.
Видео. Автор – “mycodeschool”:
При всем уважении, статья ниочем. Бинарные деревья – не обязательно деревья поиска. Поэтому “Основное правило формирования бинарного дерева в С++” не канает.
Процесс удаления узла из дерева не описан. Сбалансированные деревья тоже (упомянуть хотя бы стоило).
Спасибо! Мне очень помогает, просто написано и понятно. Учусь по Вашему сайту
Спасибо! для новичков, то что нужно.
То что надо!
Спасибо за вывод дерева, долго искал