Интерполирующий поиск

Угадайте, какое самое любимое занятие многих преподавателей? Подсказываю: Выдумывать в своих классных комнатах страшно академические словечки, чтоб у студентов волосы встали дыбом от мегаулетности его сенсея. Одно из таких коварных словечек, повергающих молодых людей в шок – Интерполяция. Предлагаю осмотреть это чудо математической мысли с самого простейшего ракурса и используя минимум кода, чтоб не мулять глаза тоннами операторов, запутывая себя в теории.

Итак, для начала – что же это за слово такое “Интерполяция”? Интерполяция – это (если говорить на языке студента) определение области поиска, путем вычисления подобия расстояний между искомым значением и всей областью. Помните по геометрии подобие треугольников? Те, у которых одинаковые по значению углы, но пропорции разные. Здесь практически тот же принцип. Вычисляется длина области поиска, и длина от начала области до некоего числа (скажем до центрального элемента в массиве). Вычисление это проводится как с номерами элемента, так и с их значениями, после чего полученная длина области умножается на длину между значениями, и результат прибавленный к значению из начала области дает искомое.

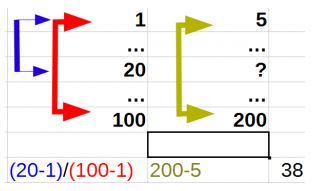
Сложно сразу понять на словах, поэтому попробую показать картинкой:

Формула достаточно проста – вычисляется длина между номерами первого элемента и искомого (задаваемого точнее). Такая же длина считается между первым и последним номерами. Длины между собой делятся, как раз и получая вычисление подобия. То же самое происходит со значениями элементов – так же вычисляется расстояние между граничными значениями в массиве. Специально выделяю цветом понятия и связанные с ними части формулы.

Полученная длина номеров элементов массива умножается на длину значений в этих (граничащих) элементах и прибавляется значение в первой ячейке массива.

Получается: 1 + (20-1)/(100-1) * (200-5) = 38 с копейками.

Результат и есть то самое искомое. Т.е. при таких значениях как на картинке в ячейке №20 будет стоять 38. Вот и весь смысл интерполяции – составления подобия между номерами элементов и между значениями элементов.

На С++ это выглядит так:

Таким образом сам цикл просто вычисляет по формуле область массива, где может находиться искомое используя этот самый принцип интерполяции в С++, подбирая подобия так сказать. Если вычисленное не равно искомому, значит нужно сдвинуть границы области, где проходит вычисление.

Если вычисленное больше – сдвигается правая граница области поиска, если меньше – левая. Так отрезая (как в бинарном поиске) кусок массива за куском постепенно достигается нужная ячейка массива, ну или границы области поиска сужаются до таких величин, в пределах которого уже искать нечего, когда дистанция между границами равна 1 (т.е. между точкой А и В нет более элементов для вычисления) решение говорит о том, что значение в массиве не найдено.

Как видите сам цикл не настолько уж и сложен и ужасен. Вся соль то скрыта в его форуме. А остальное – просто проверки: нашли или дальше искать. Вот такая вот она… интерполяция в С++

Интерполяционный поиск в чем-то напоминает двоичный. Только в нем область поиска не делится на две равные части. Вместо этого производится оценка новой области поиска по расстоянию между текущим значением элемента и ключом поиска. Скорость работы интерполирующего поиска превосходит скорость двоичного. Еще одно весомое отличие интерполирующего поиска от двоичного – возможность искать текстовую информацию, а не только числовые значения.