Решето Эратосфена – один из древнейших алгоритмов, позволяющих найти числа, которые называют “простыми”. Т.е. числа, которые могут делиться без остатка только на единицу и на себя. Например число 2. На что из натуральных (целых) чисел можно разделить 2, чтоб не получать остаток? Только на 2 и на 1. Или число 7. То же самое. Без остатка оно делится опять таки только на себя и единицу.
Достаточно простой алгоритм еще до нашей эры придумал хитрый дядько Эратосфен Киренский. Грек по национальности. Математик, астроном, географ. Решето дядьки Эратосфена достаточно популярный алгоритм поиска.
Какого-то особого описания этот алгоритм на самом деле не требует. Он предполагает два цикла прохода по набору чисел. Первый определяет следующее простое число, второй вложенный в него вычеркивает все сложные числа (по определенной формуле) стоящие после этого простого. Надо сразу оговориться, что второй цикл сразу все сложные числа не вычеркивает.
Он вычеркивает следующие числа после простого, которые от этого простого находятся на определенном расстоянии. Расстояние это рассчитывается по формуле: Текущий элемент в квадрате + значение этого элемента.
Например если число 5 простое, то следующее после него, которое стоит вычеркнуть будет равно 5*5 = 10, потом 5*5+5 = 15,потом 5*5+5+5 = 20… и так далее. Вычеркиваются таким образом числа кратные этому найденному простому. Нахождение простого начинается с числа 2. Соответственно вычеркиваются 2*2, 2*2+2, 2*2+2+2…
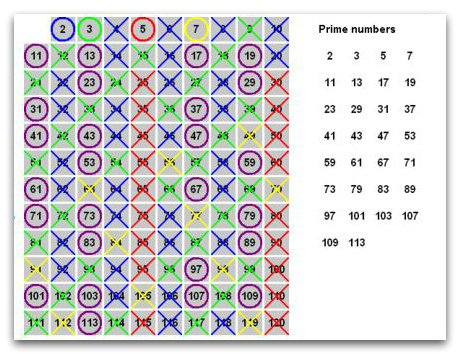
Хорошая иллюстрация есть на сайте Википедии:
Берем первое простое число 2 (синий кружочек) и вычеркиваем все числа, которые кратны двум (синие крестики). Потом берем простое число 3 (зеленый кружочек) и вычеркиваем все что ему кратно (зеленые крестики) и т.д.
После того, как числа вычеркнуты из списка легко определить следующее простое число – оно будет первое не вычеркнутое после текущего.
Поскольку сам код не очень то и большой, я не буду разбивать его на блоки, там нечего то и конкретизировать. Выглядит он к примеру так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | #include <iostream> using namespace std; int main() { int n = 100; //Считать числа до этого //Запрашиваем массив int *a = new int[n + 1]; //Наполняем его числами для решета for (int i = 0; i <= n; i++) a[i] = i; //*********************************************************** //Проводим главный цикл. - Начало работы решета for (int i = 2; i * i <= n; i++) { if (a[i]) //Если текущее число не равно 0 - начинаем от него искать сложные for (int j = i*i; j <= n; j += i) //И обнуляем их ячейки, чтобы больше не проверять их в цикле a[j] = 0; } // Решето окончило отсев - в массиве остались только простые //************************************************************ //Выводим необнуленные - простые for (int i = 2; i < n; i++) { if (a[i]) { cout << a[i] << ' '; } } cout << endl << endl; delete[] a; //И освобождаем массив return 0; } |
Работает сей код следующим образом: Запрашивается массив чисел. Я специально для удобства добавил к массиву один “вспомогательный” элемент в конец, чтоб программа начинала работать с массивом не с нуля, как принято отсчитывать в С++ массивы, а с единицы.
Для наглядности естественно. После запроса массив заполняется числами по порядку. Можно было конечно не использовать массив чисел, а просто массив булевых (true, false), и простыми числами считать номера элементов, которые после просеивания будут содержать true, но я решил, что это не так наглядно.
После того, как числа в массиве размещены (1,2,3,4,5,6,7,8,9,10…n) можно приступать к их просеиванию. Пока что на начальном этапе все числа в решете считаются программой простыми. Первая итерация цикла берет первое (а точнее второе по счету) число – 2. От этого числа второй цикл обнуляет элементы массива, которые попадают под фильтр-условие Число*Число+Число.
Таким образом просеиваются числа кратные двум после двойки. Далее первый цикл продолжает проход, проверяя условие if(a[i]) , т.е. есть ли в ячейке число, отличающееся от нуля (мы ведь обнуляем сложные числа). Как только такое число будет найдено, опять уже от него сработает второй цикл, обнуляя после найденного кратные ему числа, стоящие после него.
И так циклы просеивают числа пока не достигнут заданной нами границы просеивания – до какого числа вылавливать простые.
Где используются простые числа? Хм… Например в криптографии. Так же в некоторых генераторах случайных чисел. Ну и конечно же в ВУЗах :) По сути решетом преподаватели тоже не гнушаются и регулярно умело балуют студентов заданиями “Нахождения простого числа”. Вот с помощью такого решета эта задача вполне решаема.

А как реализовать отбрасывание на начальном этапе всех четных чисел кроме двойки? Чтобы потом уже среди нечетных искать простые?
“5*5 = 10, потом 5*5+5 = 15, потом 5*5+5+5 = 20…” Исправьте!