Совершенно особую группу алгоритмов составляют сортировки — сортировать в практике приходится самые разнообразные объекты и по самым разнообразным критериям. Анализ алгоритмов сортировки хорошо и обстоятельно изучен, как ни один другой раздел вычислительной математики. Основным вопросом любого алгоритма сортировки является его вычислительная сложность — число операций сравнения-обмена, требуемых для сортировки последовательности длины N, так называемое O( N ).
Неприятным обстоятельством является то, что для разных алгоритмов различаются средняя сложность (на большинстве тестовых последовательностей) и максимальная сложность (на наихудшей для метода тестовой последовательности). Для нескольких десятков алгоритмов сортировки, предлагаемых в процессе обучения программированию, показано, что подавляющее большинство из них (интуитивно понятных) является худшими и в смысле средней и в смысле максимальной сложности. Как пример, популярная у студентов пузырьковая сортировка является наихудшей из всех вообще известных.
Эффективными (по сложности) из всего множества методов являются только несколько методов быстрых рекурсивных сортировок. Они то и представлены в реализациях алгоритмов STL. Стандарты не настаивают на жёстком ограничении на внутренних механизмах их реализации, поэтому могут быть варианты в зависимости от используемой библиотеки.
Теперь, обладая некоторыми знаниями об алгоритмах, функторах и общем состоянием дел с сортировками, мы готовы рассмотреть варианты реализации всего этого в своём коде. Для начала мы разнообразными способами сортируем числовые последовательности. Пример великоват, но он предназначен не только, и не сколько, для иллюстрации, как для последующего самостоятельного экспериментирования:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | #include <iostream> #include <vector> #include <cmath> #include <algorithm> #include <ctime> using namespace std; vector<unsigned> create( int size, char mode = '-' ) { // заполнить в указанном порядке vector<unsigned> vect = vector<unsigned>( size ); unsigned j = 0; if( '?' == mode ) srand( (unsigned int)time( NULL ) ); for( vector<unsigned>::iterator i = vect.begin(); i != vect.end(); i++ ) switch( mode ) { case '+' : *i = ++j; break; case '?' : *i = nearbyint( (double)rand() / RAND_MAX * ( size - 1 ) ) + 1; break; case '-' : default : *i = size--; break; } return vect; } bool test( vector<unsigned>& v ) { // финальный контроль монотонности bool dir = v[ 0 ] < v[ 1 ]; // порядок сортировки vector<unsigned>::iterator i = v.begin(); while( true ) { auto j = i; if( ++j == v.end() ) break; if( ( *i <= *j ) != dir ) return false; i++; } return true; } typedef void (sort_func)( vector<unsigned>& ); // предварительные объявления функций сортировки: sort_func sort1, sort2, sort3, sort4, sort5, sort6; sort_func* variants[] = { sort1, sort2, sort3, sort4, sort5, sort6 }; ostream& operator <<( ostream& stream, vector<unsigned>& v ) { // отладка-контроль stream << "[ "; for( auto x : v ) stream << x << " "; return stream << "]"; } int main( int argc, char *argv[] ) { if( argc < 3 ) return 1; char *parm = argv[ 1 ]; // длина и порядок тест-последовательности char mode = *parm == '-' || *parm == '+' || *parm == '?' ? *parm++ : '-'; int size = atoi( parm ); if( size <= 0 ) return 2; int debug = 0; parm = argv[ 2 ]; // вариант и уровень отладки while( '+' == *parm ) debug++, parm++; unsigned var = atoi( parm ); if( var > 0 && var <= sizeof( variants ) / sizeof( variants[ 0 ] ) ) var--; else return 3; vector<unsigned> vect = create( size, mode ); if( debug ) cout << vect << endl; variants[ var ]( vect ); if( debug ) cout << vect << endl; else cout << ( test( vect ) ? "OK" : "not OK" ) << endl; } //-------------------------------------------------------------------------------------------- // Быстрая сортировка. Сложность в среднем O( n*log(n) ), но в худшем случае O( n*n ) void sort1( vector<unsigned>& v ) { sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- bool sort_function( unsigned f, unsigned s ) { return f > s; } void sort2( vector<unsigned>& v ) { // использование функции как предикакта sort( v.begin(), v.end(), sort_function ); }; //-------------------------------------------------------------------------------------------- struct sort_class { // функтор сравнения bool operator()( unsigned f, unsigned s ) { return f > s; } }; void sort3( vector<unsigned>& v ) { sort( v.begin(), v.end(), sort_class() ); }; //-------------------------------------------------------------------------------------------- // Сортировка подпоследователности. Гарантированная сложность O( n*log(n) ) в любом случае. // Обычно сортировка в куче выполняется в 2-5 раз медленнее быстрой сортировки sort(). void sort4( vector<unsigned>& v ) { partial_sort( v.begin(), v.end(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка слиянием. Сложность O( n*log(n) ) или O( n*log(n)*log(n) ), если без дополнительной памяти void sort5( vector<unsigned>& v ) { stable_sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка в куче (heap) - вызывают функции, непосредственно работающие с кучей // (то есть с бинарным деревом, используемым в реализации этих алгоритмов). // Сложность O( n+n*log(n) ) void sort6( vector<unsigned>& v ) { make_heap( v.begin(), v.end() ); sort_heap( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- |
Перед компиляцией программы, в MVS нажмите Alt+F7 и внесите Аргументы команды ?30 +3: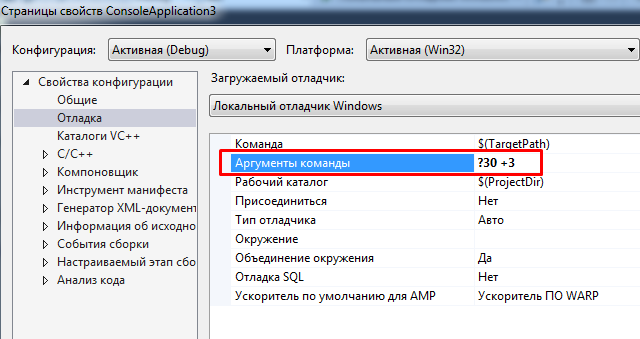
Некоторая громоздкость примера связана с тем, что мы в одном коде объединяем и все предоставленные STL алгоритмы сортировки, и разнообразные тестовые сортируемые последовательности, например:
Несколько случайных (?) последовательностей длины 30, сортируемых с использованием (3) функтора сравнения, и детализированным (+) выводом входной и выходной последовательности:

Инверсная (обратная, убывающая) последовательность, сортируемая (6) «в куче» с использованием бинарного дерева (аргументы команды -30 +6 ):

Длинная (1000000) последовательность, в тех же, что и предыдущий случай, условиях, но с выводом только диагностики корректности результата (аргументы команды -1000000 6 ):

Библиотека STL предоставляет 3 группы алгоритмов сортировки:
sort() – наиболее быстрая сортировка в среднем ( O( N * log( N ) ), но которая может «проваливаться» в худшем случае до O( N * N ) (а это очень плохой показатель);
sort_heap() – сортировка в «в куче», с использованием бинарного дерева, сложность которой всегда не хуже O( N + N * log( N ) ) (это хуже sort() в среднем, но лучше в наихудшем случае);
stable_sort() – «устойчивая» сортировка слиянием, устойчивость которой означает, что она сохраняет относительный порядок равных элементов после сортировки. Это иногда очень важно. Сложность этого алгоритма не намного уступает sort();
Используйте тот алгоритм, который наиболее соответствует ограничениям вашей задачи.