Гипотеза Коллатца – это одна из нерешённых проблем в математике с 1937 года (Гипотеза Коллатца, Collatz conjecture), которую математики не могут ни доказать, ни опровергнуть. Гипотеза состоит в том, для любого натурального числа n>1 последовательное применение функции:


– приведёт к числовому ряду, который, в конечном итоге (рано или поздно) приведёт к числу 1 (то есть, на каждом шаге преобразований для чётных значений следующим шагом вычисляется n/2, а для нечетных – 3n+1). Например, для n=3 это будет ряд преобразований: 3,10,5,16,8,4,2,1. Для некоторых n эта последовательность чисел будет весьма короткой, но для некоторых – очень длинной…
Наше задание не в том, чтобы решить задачу, которую все математики мира не могут решить 80 лет, а в том, чтобы для любого n построить цепочку числовых для такого преобразования (то, что математики называют: чи́сла-гра́дины).
Конечно, как и раньше, одним из критериев качества решения будет: код должен быть записан как можно короче.
Решение.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include <iostream> #include <sstream> using namespace std; // гипотеза Коллатца void collatz( unsigned long val ) { cout << val << " => ["; while( true ) { val = val & 1 ? 3 * val + 1 : val >> 1; cout << val << ( val > 1 ? "," : "]\n" ); if( 1 == val ) return; } } int main() { setlocale(LC_ALL, "rus"); string e; unsigned long d; while( true ) { cout << "Вводите натуральные числа: "; getline( cin, e ); istringstream ist( e ); while( ist >> d ) collatz( d ); } } |
Как это выполняется:
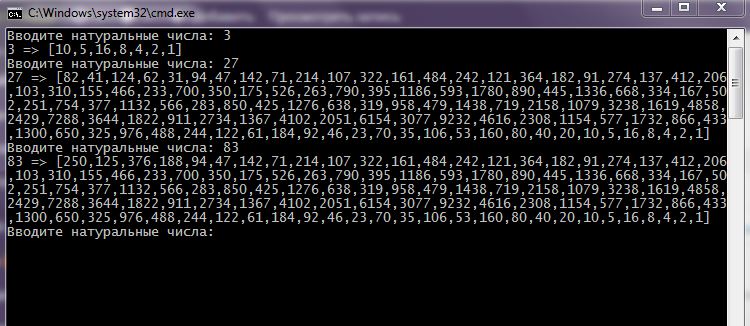
#include
using namespace std;
int main() {
setlocale(LC_ALL, “rus”);
long all = 1;
cin >> all;
for (;;) {
if (all % 2 == 0) {
all /= 2;
cout << all << endl;
}
else {
all = (all * 3) + 1;
cout << all << endl;
}
if (all == 1) {
break;
}
}
system("pause");
return 0;
}
Николай, типа у тебя короче?
Ладно про проверку чётности и деление на 2 делением, х с ним.
Но ты бы хоть вывод не дублировал.