In C ++ any function except main() can call itself. That is, in the body of the function can be placed a call to this same function. This is called recursion.
When the program executes the code of a recursive function– she will perform it indefinitely, if you do not provide a condition to exit the recursion. This should be remembered, to avoid looping calls. Therefore, in the definition of recursive function must specify the exit condition. For example, You can place it inside the block call if.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(9); return 0; } |
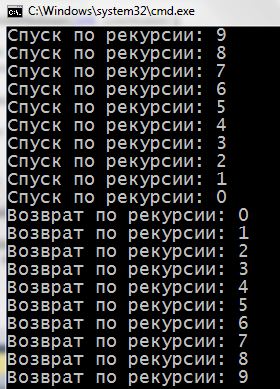
In this program functionrecursionGoDown() will call itself, until it is transferred to a number greater than zero. Every time, function gets the number of, from which is subtracted in the signature unit. As soon as the condition becomes false (the number will be less than zero) – calls to stop and start the output of the recursion.
If we pass in a function number 9, calls will 10. The program as it deepens on 10 levels, performing recursion. To her out of the recursion, We must pass these ten levels back. So the string of code
1 | cout << "Возврат по рекурсии: " << someNumber << endl; |
will run too 10 times, but the valuesomeNumberwill change in the opposite order. First, it will conform to, that was passed to the function by 10 levels of recursion, then passed on to the fact that 9 level, etc..
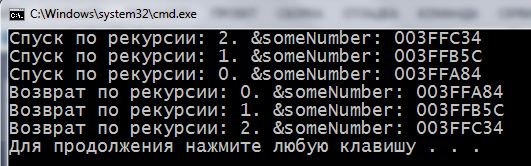
I want to draw attention to an important point. Each recursive call creates a new variable someNumber with the new value. These variables will occupy some space in RAM. If the call 10, as in our example, and it will be stored in the memory 10 with different values of the variables. It is possible to add to the program output to the screen addresses, which stores these values and see this:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream> using namespace std; void recursionGoDown(int someNumber) { cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber << endl; if (someNumber > 0) { recursionGoDown(someNumber - 1); // рекурсивный вызов } cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl; } int main() { setlocale(LC_ALL, "rus"); recursionGoDown(2); return 0; } |
Passing in a function number 2: recursionGoDown(2); Levels of recursion is 3.
As seen, each value of a variable someNumber stored in a separate memory segment. During the return to recursion values come from the same addresses but in reverse order.
Almost every task, which can be solved using recursion, can be implemented using iteration loops. You can in fact easy to show on the screen the number of 9 to 0 and by 0 to 9 applying loops. In addition, you should know, that recursion takes more memory and calculation will produce slower, than the iteration.
But, as claimed by experienced programmers and many authors of books, this does not mean, recursion is useless. There are tasks, decide which, using iteration loops, difficult and cumbersome. A recursive solution looks better. For entry-level, until you learn only basics of programming in C ++, you just need to understand, what a recursion is and how it works.
See more videos about Recursion:
You're too hard on recursion ;-)
1. Recursion – a general mathematical formalism, which theoretically express all computable algorithms (I took it from the mat. theory of algorithms).
2. All tasks of dynamic data structures (lists, queue, trees, counts, …) solved recursively easier, and most importantly clearer, than iteratively (cyclic iterative algorithms work better on arrays – static structures).
3. There are algorithms, expressed in 2-3 line recursively, but that is very difficult to write without recursion. A beautiful example of this: famous challenge “tower of Hanoi”. Many sorting algorithms (the same array) better expressed in a recursive form.
Recursion just seems complicated, because it is not taught in the domestic practice and do not know how to use it. And at universities in France, for example, training 1st semester starts with learning recursive algorithms.
Always good, when someone expresses his point of view and my personal opinion, based on experience. Beginners will be useful to read.
How do you propose to use recursion in lists and queues?
Recursion – this is most natural way to handle any dynamic structures (lists, trees, etc.), This exhibit functional programming languages, such as Lisp. This approach is much more effective, than iterative (cycles). But it should be shown on code examples…
A simple and beautiful example of recursion look at the problem of a number raised to a power: https://purecodecpp.com/archives/2734
Hello.
Please explain the following points, All head broke, can not understand:
1. If you do not take exactly the array in the fission process in the sub-arrays on 2, the program will stop working? Indeed, in int middle = arr[(l+r)]/2 , Where (l+r)/2- integer.
2. If the array contains duplicate numbers, and the support member will be the same number of, like the number to the left or right, for example 1,2,3, 5, 6,5,7
then, that will not work after, as the program defined central element 5 =, and beginning its comparison with the elements of the right subarray , it reached the same element arr [5]= 5 think that reached the central element , cease to compare the earlier elements (arr [4}, arr [3]) with central, take this 5 for the central element, and will continue to consider it at the left border?
3. In the example considered pairwise change (the left and right of the central) elements, not udovletoryayuschih condition:
while (middle>arr [i]) i ;
while (middle<arr [j]) j–;
if (i<=j)
{
swap (arr [i], arr [j]);
i ;
j–;
}
What if either initially, or after the sorting process remains 1
element to be replaced, for example:
1, 2, 3, 8, 5, 6, 7, 9,10
then if I understand correctly, it changes from a central element,
i.e.. succeed 1,2,3,5, 8, 6,7,9,10 ?
4.
The value of the central element may vary. At the same time, after the change of the central element, comparison, produced with the earlier central element prove incorrect, they are not unnecessarily reviewed, and continue to move on. As a result, sorting would be wrong.
For example:
source array: 1,2,6,9, 4, 10,11,3, 12 a central element 4.
Since first replacement (6 on 3) obtained: 1,2,3,9, 4, 10,11,6,12.
After the second replacement (9 on 4) obtained: 1,2,3,4, 9, 10,11,6,12 and sorting of the set ends with. However, right subset element 6 sorted incorrectly.
interesting, I mastered recursion and now I have already begun to solve problems on this topic from the site acmp.ru, and I came across such a task:
Sum of cubes
(Time: 1 sec. Memory: 16 MB complexity: 52%)
It is known, that any natural number can be represented as a sum of at most four squares of natural numbers. Vasya decided to come up with a similar statement for cubes – he wants to know, how many cubes are enough to represent any number. His first working hypothesis – eight.
It turned out, that almost all numbers, which Vasya could come up with, are represented as a sum of no more than eight cubes. However, the number 239, for example, does not allow such a representation. Now Vasya wants to find some other such numbers, and, perhaps, any pattern in the representations of all other numbers, to hypothesize about the kind of all numbers, which are not represented as a sum of eight cubes.
Help Vasya write a program, which would check, is it possible to represent a given natural number as a sum of no more than eight cubes of natural numbers, and if possible, would find any such representation.
Input data
The input file INPUT.TXT contains a natural number N (1 ≤ N ≤ 2×109).
Output
Print to the output file OUTPUT.TXT no more than eight natural numbers in non-increasing order, whose cubes add up to N. If there are several options, then output any. If the required representation does not exist, then the word IMPOSSIBLE must be output to the output file.
examples
№ INPUT.TXT OUTPUT.TXT
1 17 2 2 1
2 239 IMPOSSIBLE
I thought that dp and even wrote the code, and later I realized that a vector of this size simply does not exist, please help to solve this problem
Unclear, why does recursion start producing values in reverse order, there is nothing like that in the code:
void recursionGoDown(int someNumber)
{
cout << "Спуск по рекурсии: " << someNumber << ". &someNumber: "<< &someNumber < 0)
{
recursionGoDown(someNumber – 1); // рекурсивный вызов
}
cout << "Возврат по рекурсии: " << someNumber << ". &someNumber: " << &someNumber << endl;
}
In theory, as soon as someNumber is made equal 0, the condition of the if statement becomes false and the block {recursionGoDown(someNumber – 1);} should just be ignored. But instead it's executed in reverse. How this shit works???
QHT9A9
0kobwr