We have already dealt with the algorithm linear search. In the same article mentioned, that is not the only algorithm, which makes it possible to find the target value of the array. Existother search algorithms. Binary (binary) search is more efficient (checked asymptotic analysis of algorithms) the decision in the case, if the array is sorted in advance.
Supposing, the array of 12 elements sorted ascending:
The user sets the desired value (search key). Let's 4. On the first iteration array It is divided into two parts (We are looking for the middle element – midd): (0 + 11) / 2 = 5 (0.5 discarded). At first, checks the value of the middle element of the array. If it coincides with a key – the algorithm terminates and the program displays the message, that value is found. In our case, the key does not match the value of the middle item.
If the key is less than the average member, the algorithm will not be searched in one half of the array, which contains a value greater than the key (i.e.. from the middle to the end of the array element). The right edge of the search moves (midd – 1). Then again on the array division 2.
The key again is not equal to the middle element. It's more him. Now the left border of the search moves (midd + 1).
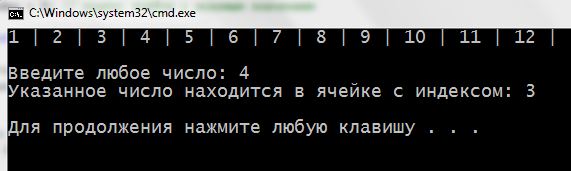
The third iteration of the middle element – a cell index 3: (3 + 4) / 2 = 3. It is the key. The algorithm terminates.
Example:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | #include <iostream> using namespace std; // функция с алгоритмом двоичного поиска int Search_Binary (int arr[], int left, int right, int key) { int midd = 0; while (1) { midd = (left + right) / 2; if (key < arr[midd]) // если искомое меньше значения в ячейке right = midd - 1; // смещаем правую границу поиска else if (key > arr[midd]) // если искомое больше значения в ячейке left = midd + 1; // смещаем левую границу поиска else // иначе (значения равны) return midd; // функция возвращает индекс ячейки if (left > right) // если границы сомкнулись return -1; } } int main() { setlocale (LC_ALL, "rus"); const int SIZE = 12; int array[SIZE] = {}; int key = 0; int index = 0; // индекс ячейки с искомым значением for (int i = 0; i < SIZE; i++) // заполняем и показываем массив { array[i] = i + 1; cout << array[i] << " | "; } cout << "\n\nВведите любое число: "; cin >> key; index = Search_Binary (array, 0, SIZE, key); if (index >= 0) cout << "Указанное число находится в ячейке с индексом: " << index << "\n\n"; else cout << "В массиве нет такого числа!\n\n"; return 0; } |
Result:
The binary search algorithm is effective - his assessment of the complexity of O(log2(n)), while an ordinary incremental search O(n). It means, that for example, for an array of 1024 elements of linear search in the worst case (when the desired item is not in the array) process all 1024 elements, but a binary search is enough to handle the log2(1024) = 10 elements. This result is achieved due to the fact, that after the first step, the search area is narrowed to loop 512 elements, After the second – to 256 etc.
The disadvantages of such an algorithm is the requirement of ordering data, as well as the ability to access any data element for the continued (independent of the number of data) time. Thus, the algorithm can not work on any disordered arrays and data structures, built on the basis of linked lists.
See also, how to implement binary search algorithm in C.




Thank you. Very detailed and very clear beginner….
In the example, the error code, if you enter, for example, number 13, the latest iteration is already abroad array(midd = 12). The program does not fall and gives the correct result, because abroad there is an array of memory available to the process.
int midd = 0;
while (1)
{
if(midd <=n)
{
midd = (left + right) / 2;
if (key arr[midd]) // If desired more value in the cell
{
left = midd + 1; // Search displace left border
}else // otherwise (значения равны)
{
cout<<"key[ "<<midd<<" ] = "<<key<<endl;
return midd; // function returns the index of the cell
}
}
} return -1;
}
Fixed, like, if not difficult to verify
if(midd <=n)
n — what's this?
n - is that? it's your value that you are looking for in the array
For example an array of 20 numbers
Why did I enter in the search for the n-Noe number
I indicates the index before him?
Because in c ++ the indexing is null (that is, the first element for a person – this is the zero element for the language, second element for human – this is the first element for the language, etc.)
All right, All right, All right “Указанное число находится в ячейке с индексом: …” All right 2, All right 3, All right, not from unit