Досить часто на практиці потрібно контролювати тільки приналежність тих чи інших об'єктів до деякій підмножині. Такі колекції і в класичній математиці називаються безліч, до якого конкретний об'єкт може або належати, чи ні. І бібліотека STL надає такий вид контейнерів, який так і називається - комплект<> (безліч).
Кожен елемент контейнера комплект<> містить тільки значення ключа (не кілька, як для карта<>), тому такий тип контейнера дуже ефективно реалізує операцію перевірки наявності значення в наборі. Цей контейнер надає багато спільних методів в порівнянні карта з<>, хоча вони тут мають деякі вироджені якості (і часом непотрібні):
операція вставки (метод вставити()) нового значення ключа до безлічі повертає пару типу <итератор, bool> (просто, як для карта<>). У цій парі другий компонент (second, типу bool) вказує на успішність операції: якщо це true, то перший компонент повертається результату (first) дає итератор нового доданого елемента. Але це досить безглузде повертається значення: якщо повертається true, то нове значення успішно додано до безлічі, якщо ж повертається false, то воно вже присутній в безлічі раніше - в обох випадках кінцевий стан безлічі буде ідентичним (тому на практиці значення, що повертається вставити() зазвичай навіть не перевіряють ... а багато хто і не знають, що там взагалі передбачено повертається значення взагалі);
Для цього контейнера реалізований метод count() (як для MultiMap<>), але, оскільки значення ключа може бути присутнім в множин тільки в одиничному екземплярі, метод count() може повернути тільки 0, якщо таке значення відсутній, і 1 коли таке значення присутній.
Для контейнера реалізований метод знайдений(), який повертає итератор элемента, якщо значення знайдено, і итератор зі значенням end() якщо значення відсутній в безлічі.
Для демонстрації сказаного створимо додаток, яке N раз (параметр, задається в команді запуску додатка) в циклі генерує псевдовипадкове число в фіксованому діапазоні [0…іт] і поміщає його в безліч. Понятно, що при зростанні N більше ніж lim (а тим більше при N набагато більше lim), кожне число діапазону[0…іт] буде генеруватися все більше і більше число раз:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #include <iostream> #include <cstdlib> #include <iomanip> #include <cmath> #include <set> using namespace std; int main( int argc, char **argv ) { unsigned lim = 30, n = argc > 1 ? atoi( argv[ 1 ] ) : lim; set<unsigned> rnd; for( unsigned i = 0; i < n; i++ ) { rnd.insert( (unsigned)nearbyint( (float)rand() / RAND_MAX * ( lim - 1 ) ) ); } cout.fill( '0' ); for( unsigned i = 0; i < lim; i++ ) { if( 1 == rnd.count( i ) ) cout << setw( 2 ) << i << " "; else cout << "- "; } cout << endl; for( auto i = rnd.begin(); i != rnd.end(); i++ ) cout << setw( 2 ) << *i << " "; cout << endl; } |



Іншим близьким типом контейнера є мультімножество<>, що дозволяє кожному значенню ключа бути не унікальним, і перебувати в безлічі скільки завгодно раз. Ці два контейнера (комплект<> і мультімножество<>) настільки подібні, що в показаному вище додатку ми замінимо всього 2 рядки (метод count() для мультімножество<> возвращает число входжень значення в безліч):
1 2 3 4 | ... multiset<unsigned> rnd; ... if( rnd.count( i ) > 0 ) cout << setw( 2 ) << i << " "; |
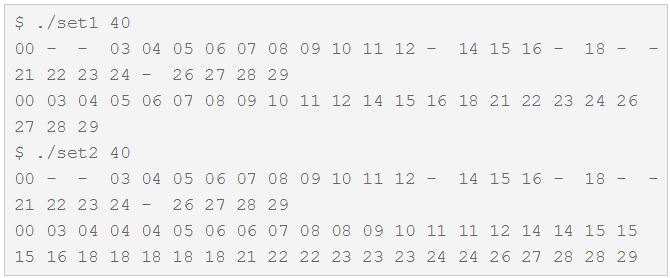
Але поведінка додатки радикально змінюється (для порівняння поруч показані результати 2-х додатків в ідентичних умовах):
Видим, що для мультимножини значення 1, 2, 13, 17… відсутні в контейнері, а значення 18, например, присутній в ньому 5 раз.
s5gxsl