It is a special group of sorting algorithms make - in practice it is necessary to sort a variety of objects and on a variety of criteria. An analysis of sorting algorithms are well and thoroughly studied, More than any other section of Computational Mathematics. The main issue of any sorting algorithm is its computational complexity - the number of comparison-exchange operations, required for sorting a sequence of length N, so-called O( N ).
The unpleasant fact is that, that the average complexity of different algorithms for different (on most test sequences) and the maximum complexity (at worst for a method of test sequence). For several tens of sorting algorithms, offered in learning Programming, shown, that the vast majority of them (intuitive) It is the worst in terms of average and in terms of maximum complexity. As an example,, popular among students bubble sorting It is the worst of all generally known.
Effective (complexity) the entire set of methods are only a few methods of fast recursive sorting. They are then presented to the STL implementations of algorithms. Standards do not insist on a hard constraint on domestic mechanisms for their implementation, therefore it may be possible depending on the library.
Now, having some knowledge about algorithms, functor and the general state of affairs with sorting, we are ready to consider options for implementing all this in your code. To start a variety of ways we sort numeric sequence. An example is too big, but it is not only, and as, to illustrate the, for subsequent self-experimentation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 | #include <iostream> #include <vector> #include <cmath> #include <algorithm> #include <ctime> using namespace std; vector<unsigned> create( int size, char mode = '-' ) { // заполнить в указанном порядке vector<unsigned> vect = vector<unsigned>( size ); unsigned j = 0; if( '?' == mode ) srand( (unsigned int)time( NULL ) ); for( vector<unsigned>::iterator i = vect.begin(); i != vect.end(); i++ ) switch( mode ) { case '+' : *i = ++j; break; case '?' : *i = nearbyint( (double)rand() / RAND_MAX * ( size - 1 ) ) + 1; break; case '-' : default : *i = size--; break; } return vect; } bool test( vector<unsigned>& v ) { // финальный контроль монотонности bool dir = v[ 0 ] < v[ 1 ]; // порядок сортировки vector<unsigned>::iterator i = v.begin(); while( true ) { auto j = i; if( ++j == v.end() ) break; if( ( *i <= *j ) != dir ) return false; i++; } return true; } typedef void (sort_func)( vector<unsigned>& ); // предварительные объявления функций сортировки: sort_func sort1, sort2, sort3, sort4, sort5, sort6; sort_func* variants[] = { sort1, sort2, sort3, sort4, sort5, sort6 }; ostream& operator <<( ostream& stream, vector<unsigned>& v ) { // отладка-контроль stream << "[ "; for( auto x : v ) stream << x << " "; return stream << "]"; } int main( int argc, char *argv[] ) { if( argc < 3 ) return 1; char *parm = argv[ 1 ]; // длина и порядок тест-последовательности char mode = *parm == '-' || *parm == '+' || *parm == '?' ? *parm++ : '-'; int size = atoi( parm ); if( size <= 0 ) return 2; int debug = 0; parm = argv[ 2 ]; // вариант и уровень отладки while( '+' == *parm ) debug++, parm++; unsigned var = atoi( parm ); if( var > 0 && var <= sizeof( variants ) / sizeof( variants[ 0 ] ) ) var--; else return 3; vector<unsigned> vect = create( size, mode ); if( debug ) cout << vect << endl; variants[ var ]( vect ); if( debug ) cout << vect << endl; else cout << ( test( vect ) ? "OK" : "not OK" ) << endl; } //-------------------------------------------------------------------------------------------- // Быстрая сортировка. Сложность в среднем O( n*log(n) ), но в худшем случае O( n*n ) void sort1( vector<unsigned>& v ) { sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- bool sort_function( unsigned f, unsigned s ) { return f > s; } void sort2( vector<unsigned>& v ) { // использование функции как предикакта sort( v.begin(), v.end(), sort_function ); }; //-------------------------------------------------------------------------------------------- struct sort_class { // функтор сравнения bool operator()( unsigned f, unsigned s ) { return f > s; } }; void sort3( vector<unsigned>& v ) { sort( v.begin(), v.end(), sort_class() ); }; //-------------------------------------------------------------------------------------------- // Сортировка подпоследователности. Гарантированная сложность O( n*log(n) ) в любом случае. // Обычно сортировка в куче выполняется в 2-5 раз медленнее быстрой сортировки sort(). void sort4( vector<unsigned>& v ) { partial_sort( v.begin(), v.end(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка слиянием. Сложность O( n*log(n) ) или O( n*log(n)*log(n) ), если без дополнительной памяти void sort5( vector<unsigned>& v ) { stable_sort( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- // Сортировка в куче (heap) - вызывают функции, непосредственно работающие с кучей // (то есть с бинарным деревом, используемым в реализации этих алгоритмов). // Сложность O( n+n*log(n) ) void sort6( vector<unsigned>& v ) { make_heap( v.begin(), v.end() ); sort_heap( v.begin(), v.end() ); }; //-------------------------------------------------------------------------------------------- |
Before compiling the program, in MVS press Alt + F7 and enter command arguments ?30 +3: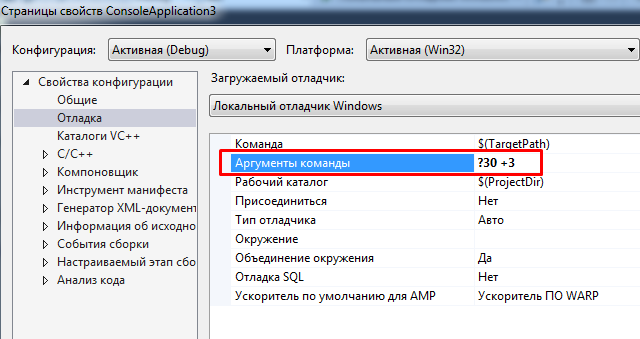
Some awkwardness example due to the fact, that we are in the same code and combine all provided STL sorting algorithms, and a variety of test sorted sequence, for example:
Several random (?) sequences of length 30, sortable using (3) functor comparison, and detailed (+) terminal input and output sequences:

Inverted (reverse, decreasing) sequence, sortable (6) "Heap" using a binary tree (arguments to -30 +6 ):

long (1000000) sequence, the same, the previous case, conditions of, but only with the conclusion of correctness of the diagnosis results (Case team -1000000 6 ):

The STL offers 3 Group sorting algorithms:
sort() – the fastest sorting on average ( O( N * log( N ) ), but which can "fall" in the worst case to O( N * N ) (and it is a very poor indicator);
sort_heap() – sorting "on the heap", using a binary tree, whose complexity always no worse than O( N + N * log( N ) ) (it worse sort() average, but rather the worst case);
stable_sort() – "Stable" merge sort, which means stability, that it maintains the relative order of equal elements after sorting. It is sometimes very important. The complexity of this algorithm is much inferior sort();
Use the algorithm, which is most consistent with the constraints of your problem.