Sieve of Eratosthenes – one of the oldest algorithms, allows you to find the number, termed “simple”. That is. number, which are evenly divisible by one and only the. For example the number of 2. What natural (as much as) numbers can be divided 2, so as not to get the rest of? Just on 2 and 1. Or the number of 7. Same. No residue is divided again only by itself and one.
Enough simple algorithm even before BC came up with a cunning uncle Eratosthenes Kirensk. Greek nationality. Mathematics, astronomer, geographer. Sieve of Eratosthenes guys quite popular search algorithm.
What a special description of this algorithm is not really required. It involves two loops pass on a set of numbers. The first determines the next prime number, second inserted it strikes out all the complex numbers (according to a formula) standing after this simple. It is necessary to make a reservation, that the second loop once all complex numbers are not strikes.
He strikes out the next number after a simple, that from this simple are at a certain distance. The distance is calculated by the formula: The current element in the square + value of this item.
For example, if the number of 5 simple, then the next after him, which is equal to strike 5*5 = 10, later 5*5+5 = 15, then 5*5+5+5 = 20… and so on. Striking out in such a way that the number of multiples found simple. Finding a simple start with a number 2. Accordingly crossed out 2*2, 2*2+2, 2*2+2+2…
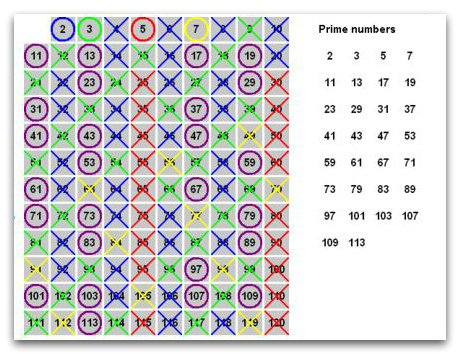
A good illustration is on the Wikipedia website:
Take the first prime number 2 (blue circle) and cross out all the numbers, which are multiples of two (blue crosses). Then take a prime number 3 (green circle) and cross out all that he is a multiple (green crosses) etc.
After, as the number removed from the list is easy to determine the next prime number – It will be the first not crossed out after the current.
Because the code itself is not very big and, I will not break it into blocks, there is nothing to it, and to specify. It looks for example so:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | #include <iostream> using namespace std; int main() { int n = 100; //Считать числа до этого //Запрашиваем массив int *a = new int[n + 1]; //Наполняем его числами для решета for (int i = 0; i <= n; i++) a[i] = i; //*********************************************************** //Проводим главный цикл. - Начало работы решета for (int i = 2; i * i <= n; i++) { if (a[i]) //Если текущее число не равно 0 - начинаем от него искать сложные for (int j = i*i; j <= n; j += i) //И обнуляем их ячейки, чтобы больше не проверять их в цикле a[j] = 0; } // Решето окончило отсев - в массиве остались только простые //************************************************************ //Выводим необнуленные - простые for (int i = 2; i < n; i++) { if (a[i]) { cout << a[i] << ' '; } } cout << endl << endl; delete[] a; //И освобождаем массив return 0; } |
This code works as follows:: Requesting an array of numbers. I specifically for the convenience of one added to the array “subsidiary” in end member, The program begins to work with an array from scratch, as it is accepted to count in C ++ arrays, and a unit.
For clarity, naturally. After the request is filled with an array of numbers in order. You could of course do not use an array of numbers, but simply an array of boolean (true, false), and primes considered item numbers, which will contain after sieving true, but I decided, that it is not clearly.
After, the numbers are placed in an array (1,2,3,4,5,6,7,8,9,10…n) you can start their screening. While the initial phase of all the numbers in a sieve are considered simple program. The first iteration of the loop takes first (or rather the second account) number – 2. From this number, the second loop resets the array elements, which fall under the filter condition * Number of Number of Number +.
Thus the number of multiple screened after two deuces. Next, the first loop continues to run, checking the condition if(a[i]) , i.e.. whether there is a cell number, different from zero (because we zero out the complex number). Once a number is found, again have him work the second loop, zeroing after it found multiple numbers, standing after him.
And so the number of loops is screened until they reach a specified contact sifting border – to a number of simple catch.
Where are the prime numbers? huh… For example, in cryptography. Thus, in some random number generators. And of course in the universities :) In fact sieve teachers also do not shun and regularly expertly pampered student jobs “Finding a prime number”. Here with the help of such a sieve, this problem is completely solved.

And how to implement at the initial stage discarding all even numbers except twos? To then among the odd look for simple?
“5*5 = 10, later 5*5+5 = 15, later 5*5+5+5 = 20…” correct!