interpolates search

Guess, what the most favorite pastime of many teachers? prompt: Invent in their classrooms scary academic buzzwords, to the students hair stood on end from his sensei megaescarpment. One of these insidious little words, Throws young people in shock – interpolation. I propose to examine this marvel of mathematical thought from the simplest angle and using a minimum of code, so as not to soap eyes tons operators, entangling themselves in theory.

So, to start – what is this word is “interpolation”? interpolation – this is (if you speak the language of the student) define search area, similarity by calculating distances between a desired value and the whole area. Note the similarity of triangles in geometry? They, having the same angles meaningfully, but the proportions are different. There are practically the same principle. Calculate the length of the search area, and the length from the beginning of the area to a certain number (to say the central element in the array). Calculation is performed as the element numbers, and with their meanings, after which the resulting length of the region multiplied by the length between the values, and the result of adding to the value of the start of the region gives the desired.

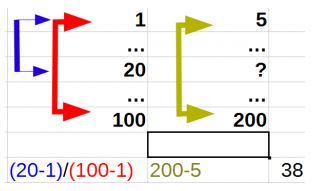
It is difficult to understand at once in words, so I try to show picture:

The formula is quite simple – calculated the length between the numbers of the first element and the desired (give the exact). The same length is considered to be between the first and last numbers. The lengths of each other are divided, just getting similarity calculation. The same happens with the values ​​of the elements – just calculated values ​​of the distance between the boundary of the array. Especially highlighted in color concepts and the associated part of the formula.

The resulting length of the array numbers is multiplied by the values ​​of the length (bordering) elements and added value in the first cell of the array.

It turns out: 1 + (20-1)/(100-1) * (200-5) = 38 kopecks.

The result is the most sought. That is. for such values ​​as in the picture in the cell №20 will stand 38. That's the whole point of interpolation – compilation of similarity between the item numbers and the values ​​between the elements.

In C ++, it looks like this:

Thus the loop itself just calculates the area using the formula array, which may be required using this same principle of interpolation in C ++, picking similarity so to speak. If the calculated is not equal to the desired, then you need to move the boundary, where the calculation of.

If calculated over – shift the right boundary of the search area, if less – the left. So cutting (how in binary search) piece by piece array gradually achieved the desired cell array, well, or the boundaries of the search area narrowed to those values, within which have nothing to look for, when the distance between the borders of equal 1 (i.e.. between the point A and have more elements to calculate) decision says, the value found in the array.

As you can see the loop itself is not so too difficult and terrible. All salt is hidden in his forum. But other – just checking: found or to seek further. Here's a she… interpolation in C ++

Interpolation search is a bit like binary. Only it is not the search region is divided into two equal parts. Instead, a new search is performed on the area of ​​assessment of the distance between the current value of the element, and the search key. The speed of the interpolation search exceeds the rate of binary. Another weighty contrast interpolating the binary search – the ability to search the text information, and not only the numerical values.