Binary trees (briefly about the main)

At all, i must admit, that the theme of hierarchical structures is very wide. About it it is possible to argue long and hard, and did not come to a common denominator, clearly shows that such a hierarchy and how to work with it, for some canons in the sense of. I will not go into the jungle of mathematical horrible Tartarus. It is no one but academics are not interested, and in the foreseeable practical too thin.

So. As an example, take binary tree wood. What tree do? This is a set of data, which point to other data. Dynamic list. Incidentally lists this particular kind of tree. Moreover, the binary.

The tree consists of branches (knots) and leaves (elements). Leaves – it hosts, which do not point at anyone, they do not have branches. binary tree – this is a tree, wherein at threads may be no more than two leaves or twigs. Hence its name – “binary” so “binary”, i.e.. or less than two elements. But not more than two.

An ordinary tree nodes in branches can be.

I will not go into the classification tree. This is also a large amount of information. This can be found in Wikipedia, what they are. You can type in a search word “Graph” and read. The main thing is not to stumble on this graph, which are the Countess. On Thursdays and Saturdays :)

The basic rule of the formation of a binary tree in C ++: If the node is greater than the added – added the right branch, otherwise a left branch.

The rule is simple, from him, and we will build. For this we need the structure of, described like a dynamic list: The data field and two pointers to the left and right branches. In dynamic lists two pointers are usually associated next and previous elements, in this case a tree with no need, because the, usually, pass on the tree is a root. Although of course can be and Feedback, if you really want.

Field Data It presents data, on the basis of which the constructed tree. More precisely one of the data elements. fields Branch describe the left and right branches of a tree, and are pointers to the same structure.

Tree items can be any value. Arrays, strings (the string is an array of characters if anything), other trees… Data fields can be many. In each field, you can build your tree. This example is from an array of characters – string.

Just show the main code tree construction, so you can understand what kind of data source is taken as an example:

String. Common string C, which will raise the branches. Units and sheets will contain characters, on codes of characters will also determine the right or to the left to construct tree. Although I took into digital characters string, it does not matter. With the same success it is possible to write a string “They killed Kenny”.

How should the work program? Take symbols “12384” from a string. First, the program sees , a tree without roots. He is not here yet. It is necessary to sow the seed, so it grew. The first character will become the root, respectively. The second character – “2” It will be compared with the root. According to the code of its value is greater than. So at the root to grow to the right branch (RightBranch) in our case. Next comes the triple. We already have two branches. The program should work through them, check: 3 more 1? – Yes. Go right. there couple. 3 more 2? Yes sir. After deuces no branches, It means it is necessary to create a branch to the right to assembly “2”.

Next comes eight. What to do with him? Same. From unit to go through a deuce to triples and just grow right branch.

After eight is 4. This value will take root. Since it is more, program should look, Do you have the right root branch. There are – go for it. Pass the “2” and “3”, for 4 More meaningfully. Further to the right to meet the number of 8. it is less than. so “4” already go from eight not right, and left.

The simplest code tree construction (with a hierarchical structure) It will look like:

Note: The functions of the three basic conditions:

1. If a branch node is not created – create it, fill the data and specify NULL (0) for its branches;
2. If the transmitted data is greater than the current node data – try to build it right branch, or if it is already there just to pass through it;
3. The same is true for the left branch, if the data value less.

Hierarchy is very friendly with recursion. Recursive call functions, to pass through the column, tree or other type of hierarchical structure – It is the easiest way. Used by the way in artificial intelligence. The above code carries a kind of search, but not for result, and to find a place for the element.

It is all! What do you think? Tree ready. Yggdrasil famous could well be established here so that's 14 th strings in C ++. Or is there some divine-cosmic language used? If you think, it is difficult to plant a tree – here's the obvious unbelievable. No. Nothing complicated there. Well, maybe N-dimensional tree will be slightly more difficult to implement…

In this case, in order to understand the principle of its construction does not need a ton of code. It is not necessary to consider the insertion between the nodes, for example to organize a tree or develop code for balancing the tree.

Naked principle in its essence is very simple. And if in the writing of a spider to surf the sites on the Internet or various 3D design programs, such as those, that develop Autodesk, knowledge trees and graphs need crazy, in the case of a simple core framework is enough and something simpler.

It remains perhaps for compliance “Feng” write traversal code and display

and the release of a tree:

Here probably seen another principle of working with trees. At print() recursively called consecutive jump from branch to branch. And between calls, data is inserted into the output node, from which branches grow, To properly display on the screen, or simply to work for example when searching for data.

The release comes as a recursive call to release branches. First, the entire left, then all right with their used and worksheets, and then freed himself calling node. It is important, because if you put delete at the beginning of the function we will get either an error (that likely) or all the branches growing from the site simply can not free, hovering in the memory garbage.

In any case, I will explain one more trick in the output:

Before the conclusion of the current node data derive a certain amount of indentation. This is done for beauty, so that the screen looks like a real tree, and not just the data set. To be able to see the structure of their own eyes.

To do this, we definea global variable int tabs=0;  that will count the number of indents, and upon (by the way!) be the bearer of values node level, i.e.. number of its nesting. How many parents of this node branches until the root. This concept can also be found in the literature about the trees. So it's there (code meaning) not only for guidance on the screen beauty.

Here is the complete code (when the tree is started “increases” not downward, as in figures, and from left to right. I do not want to complicate the code):

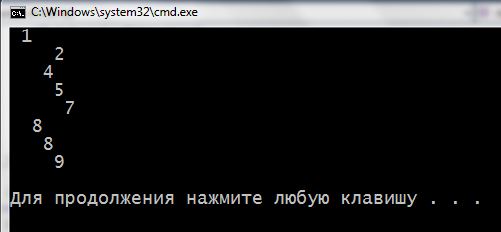
On the screen:

Well… Perhaps this about binary trees in C ++ all. How else to describe the principles of short, I do not know, but absolutely sure, that get into the wilds of academic spaces (read: prostration) not necessary. The simpler explanation is as, so it is closer to the truth.

Video. Author – “mycodeschool”: