The simple construction of the power N – is N – 1 multiplications per cycle. A multiplication – it is expensive, trudoёmkaya operation…
The wording of this task, such:
- write a function exponentiation X ** N, but, that was required for this minimum the number of multiplications);
- try to control and to include in the output number which were needed for the calculation of the multiplication.
P.S. logic of such a decision is not mine, and the famous guru Charles Anthony Hoare (Charles Anthony Richard Hoare), I just wrote down his decision code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include <assert.h> #include <iostream> using namespace std; double power(double a, int n, int& m) { assert(n > 0 || (a != 0.0 || n != 0)); switch (n) { case 0: return 1; case 1: return a; default: { double a2 = power(a, n / 2, m); if (n & 1) { m += 2; return a * a2 * a2; } else { m++; return a2 * a2; } } } } int main() { setlocale(LC_ALL, "rus"); double e, r; int n, m; while (true) { cout << "что возводить? : "; cin >> e; cout << "в какую степень? : "; cin >> n; m = 0; r = power(e, n, m); cout << e << "**" << n << "=" << r << ", число умножений " << m << endl << endl; } return 0; } |
And here are some sample performance, what should happen:
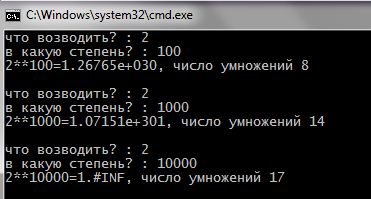
This example again shows the power of recursion as a method of calculation. Try to write this algorithm in an iterative technique (cycles) … and even better – then explain to someone how this algorithm works recorded.
love recursion!
For N ^ 15 is enough 5 multiplications. your result – 6.
And still 6. Five – this division, and this operation is more expensive (If N is not a power of two).