Collatz conjecture – It is one of unsolved problems in mathematics with 1937 of the year (Collatz conjecture, Collatz conjecture), that mathematics can neither prove, nor deny. The hypothesis is that, for any positive integer n>1 consistent application functions:


– will lead to a numeric row, which the, ultimately (Sooner or later) lead among 1 (then there are, at each step of transformation values for even the next step is calculated n / 2, and for odd – 3n+1). For example, for n = 3, it will be a number of changes: 3,10,5,16,8,4,2,1. For some n the sequence numbers will be very short, but for some – very long…
Our job is not in the, To solve the problem, that the world of mathematics can not solve 80 years, and in that, that for any n build a chain of number for this transformation (then, what mathematicians call: in the number of hailstones).
Of course, as before, one of the criteria will be the quality of solutions: code should be written as short as possible.
Decision.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include <iostream> #include <sstream> using namespace std; // гипотеза Коллатца void collatz( unsigned long val ) { cout << val << " => ["; while( true ) { val = val & 1 ? 3 * val + 1 : val >> 1; cout << val << ( val > 1 ? "," : "]\n" ); if( 1 == val ) return; } } int main() { setlocale(LC_ALL, "rus"); string e; unsigned long d; while( true ) { cout << "Вводите натуральные числа: "; getline( cin, e ); istringstream ist( e ); while( ist >> d ) collatz( d ); } } |
How it is done:
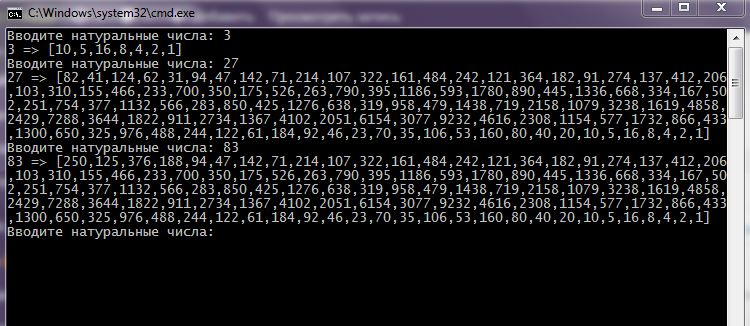
#include
using namespace std;
int main() {
setlocale(LC_ALL, “rus”);
long all = 1;
cin >> all;
for (;;) {
if (all % 2 == 0) {
all /= 2;
cout << all << endl;
}
else {
all = (all * 3) + 1;
cout << all << endl;
}
if (all == 1) {
break;
}
}
system("pause");
return 0;
}
Nikolay, like you are shorter?
Okay about parity check and division by 2 division, x with him.
But at least you would not duplicate the output.