The next, very necessary and very powerful group algorithms STL are generalized numerical algorithms (header <numeric>). This is not some kind of special computational methods, as one might think based on the name. It algorithms, allow to use the well-known library or their own computing activities to the totality of the container elements.
And because so, then they are called like all other algorithms STL. Used algorithms are generalized, mainly in mathematical calculations with respect to the containers, contains numeric elements. But this does not necessarily. And if you are not interested in the numerical calculation (for example from the field of digital signal processing), then you can just safely skip this part of the presentation…
STL's list presented generalized numerical algorithms: iota (the creation of a monotonically increasing sequence), accumulate (accumulation), inner_product (scalar multiplying the product), partial_sum (partial sum), adjacent_difference (adjacent difference).
Illustration works best to hold on to the used and intuitive algorithm accumulate. This algorithm reduces (reduces the dimension) container with the accumulation values. In particular, for simple numerical values, he turns vector<> or list<> to a single scalar result value.
Algorithm accumulate (how, however, most other) It has 2 syntactic forms:
1 2 3 4 5 | template <class InputIterator, class T> T accumulate( InputIterator first, InputIterator last, T init ); template <class InputIterator, class T, class BinaryOperation> T accumulate( InputIterator first, InputIterator last, T init, BinaryOperation binary_op ); |
In the 1st form (it is less interesting) algorithm summarizes the the value of the container elements. Do not forget at the same time, such that string, for example, operation ‘+‘ It means concatenation, gluing). In the 2nd form the algorithm collects the result of a binary operation (function of 2 variables), used to accumulate value (battery) and in turn to each of the container element.
Unclear? This powerful technique, and now everything will be clear from the example…
In mathematical statistics are used several types of average values for the numerical sequence:
Average:
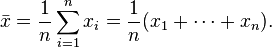
geometric mean:
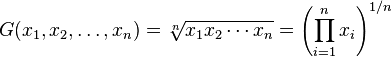
harmonic mean:
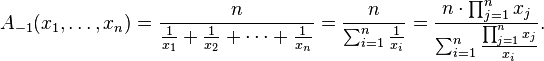
The average quadratic:
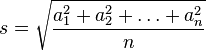
We will not delve into the meaning of each option. We will make an application, which calculates the average and some more characteristics (dispersion, standard deviation) to input a numerical sequence. The input serial input or a terminal, or redirection of pre-prepared data file:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | #include <iostream> #include <vector> #include <sstream> #include <numeric> #include <cmath> using namespace std; double amean; // среднее арифметическое (значение) double disp(double acc, double seq) { // накопление квадратов отклонений seq -= amean; return acc + seq * seq; } double mul(double acc, double seq) { // произведение элементов return acc * seq; } double garm(double acc, double seq) { // сумма обратных значений return acc + 1. / seq; } double sqr(double acc, double seq) { // сумма квадратов элементов return acc + seq * seq; } int main(void) { setlocale(LC_ALL, "rus"); string s; getline(cin, s); // читаем входную строку istringstream ist(s); // поток для чтения мз строки double d; vector<double> ser; // числовой массив while (ist >> d) ser.push_back(d); // поэлементное чтение чисел в массив int n = ser.size(); auto b = ser.begin(), e = ser.end(); amean = accumulate(b, e, 0.) / n; // сумма элементов double variance = accumulate(b, e, 0., disp) / n, deviation = sqrt(variance), gmean = exp(log(accumulate(b, e, 1., mul)) / n), rmean = n / accumulate(b, e, 0., garm), smean = sqrt(accumulate(b, e, 0., sqr) / n); cout << "ср.ариф.=" << amean << " ср.геом.=" << gmean << " ср.гарм.=" << rmean << " ср.квад.=" << smean << endl << "дисперсия=" << variance << " СКО=" << deviation << endl; } |
It is easy to see, each of complex mathematical formulas written above is calculated only on one string, using the technique of generalized algorithms:

Here we can see the well-known relation, which confirms the correctness of our calculations. It consists in the fact, that for any sequence of numbers arithmetic mean is greater than or equal to the geometric mean, which, in its turn, greater than or equal to the harmonic mean. And equality in these statements can only be achieved if all members of a sequence of numbers are equal:
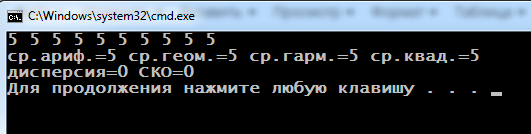
We return to the study of the code. The first call of the algorithm accumulate( b, e, 0. ) It shows the 1st form of use: container values are added to the initial value 0.0.
A warning!: Record points to the constant initial value, indicating, what is it real value - fundamentally important. Without this code will compile even without warnings, but done with completely incorrect and extremely difficult under interpretation results! This is because, algorithms that are defined as template, and the type of third parameter determines the accumulation of internal operations will be used for any type of data.
Other (4 pieces) challenges accumulate() use the 2nd form of call – 4th transmit parameter function accumulation. As seen from the examples, it takes the current parameters of the accumulated value and the next element in the container. And returns the accumulating operation. For clarity, accumulating all functions are written in the example of a simple and clear form. On practice, to avoid dependence on the type of processed data, they are also usually written, as a template function. Then it might look like this:
1 2 3 4 5 6 7 8 9 10 | template <typename T> T mul( T& acc, const T& seq ) { return acc * seq; } int main( void ) { vector<long> ser = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; cout << accumulate( ser.begin(), ser.end(), 1L, mul<long> ) << endl; } $ ./numb3 362880 |
Finally, note, if not noticed until now, that the accumulation of amounts we use the initial value 0 (3-First option accumulate() ), and the accumulation of works, naturally, 1, with the corresponding data type.
Hello!
Today looked at the online sites, where previously watched, surprise found that they do not work, that is, their movies are not broadcast at all, Tipo in your country illegally Video!
Now films do not look online for movies everywhere removed, that once again back on the torrent?
Not … just “Tipo”: hands are growing out of your ass :-(